
����Ŀ��2019���й����������ղ�����(���¼����������)��4��29����10��7���ڱ������������У�����Ϊ�����ҵ������������������4��������ɫ��Ȥ��·�ߣ��ֱ��ǣ�![]() ����������������
����������������![]() �������Ҽң���������
�������Ҽң���������![]() ������С����֮������
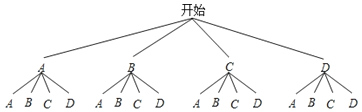
������С����֮������![]() �������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
�������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
(1)����ѡ����·![]() ������С����֮�����ĸ����Ƕ��٣�
������С����֮�����ĸ����Ƕ��٣�
(2)�û���״ͼ���б��ķ��������������ŷ�ǡ��ѡ��ͬһ��·�����ĸ��ʣ�
���𰸡�(1) ![]() ��(2)
��(2) ![]()
��������
(1)�ɸ��ʹ�ʽ���ɵó������
(2)������״ͼ������16�ֵȿ��ܵĽ�����������ŷ�ǡ��ѡ��ͬһ��·�����Ľ����4�֣��ɸ��ʹ�ʽ���ɵó������
�⣺(1)����������·��ѡһ����ÿ����ѡ�еĿ�������ͬ��
����������·�У�����ѡ����·![]() ������С����֮�����ĸ�����
������С����֮�����ĸ�����![]() ��
��
(2)����״ͼ�������£�
����16�ֵȿ��ܵĽ�����������ŷ�ǡ��ѡ��ͬһ��·�����Ľ����4�֣�
���������ŷ�ǡ��ѡ��ͬһ��·�����ĸ���Ϊ![]() ��
��


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
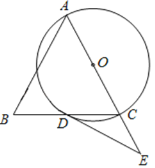
����Ŀ����ͼ����ABC�У�AB��AC����ACΪֱ������O��BC�ڵ�D����EΪAC�ӳ�����һ�㣬�ҡ�BAC��2��CDE��
��1����֤��DE����O�����ߣ�
��2����cosB��![]() ��CE��2����DE��
��CE��2����DE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���CD=CE������DE���ӳ�����F��ʹEF=AE������AF��CF������BE���ӳ���CF�ڵ�G�����н��ۣ�
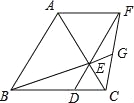
�١�ABE�ա�ACF����BC=DF����S��ABC=S��ACF+S��DCF������BD=2DC����GF=2EG��������ȷ�Ľ����� ������д������ȷ���۵���ţ�
���𰸡��٢ڢۢ�.
��������
���������������ABC�ǵȱ������Σ��ɵ�AB=AC=BC����BAC=��ACB=60�㣬����DE=DC�����ж���DEC�ǵȱ������Σ�����ED=EC=DC����DEC=��AEF=60�㣬
��EF=AE��������AEF�ǵȱ������Σ�����AF=AE����EAF=60�㣬�ڡ�ABE�͡�ACF�У�AB=AC,��BAE=��CAF,AE=AF �����ж���ABE�ա�ACF���ʢ���ȷ��������ABC=��FDC���ɵ�AB��DF��������EAF=��ACB=60�㣬�ɵ�AB��AF�������ж��ı���ABDF��ƽ���ı��Σ�����DF=AB=BC���ʢ���ȷ��������ABE�ա�ACF�ɵ�BE=CF��S��ABE=S��AFC���ڡ�BCE�͡�FDC�У�BC=DF,CE=CD,BE=CF �����ж���BCE�ա�FDC������S��BCE=S��FDC�����ɵ�S��ABC=S��ABE+S��BCE=S��ACF+S��BCE=S��ABC=S��ACF+S��DCF���ʢ���ȷ��������BCE�ա�FDC���ɵ���DBE=��EFG��������BED=��FEG���ж���BDE�ס�FGE������![]() =
=![]() ����
����![]() =
=![]() ������BD=2DC��DC=DE���ɵ�
������BD=2DC��DC=DE���ɵ�![]() =2����FG=2EG���ʢ���ȷ��
=2����FG=2EG���ʢ���ȷ��
���㣺�������ۺ���.
�����͡������
��������
19
����Ŀ���Ȼ�������ֵ��(a��1��![]() )��(
)��(![]() )������a��2��
)������a��2��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������ݣ������������⣮
С��������һ���µ����㣬ȡ��Ϊ�����ӳˣ����㣮��������������������ʽ�������£�
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
���⣺
��1������ɡ����ӳˣ���������㷨��
�������С����ӳˣ�����ʱ��________���ر�أ�0���κ������С����ӳˣ����㣬���κ�����0���С����ӳˣ����㣬________��
��2�����㣺![]() �������ŵ����������������������е�����һ�£�
�������ŵ����������������������е�����һ�£�
��3������֪���ӷ��н����ɺͽ���ɣ����������������������ġ����ӳˣ������л�����������ѡһ�������ɣ��ж����ڡ����ӳˣ��������Ƿ����ã���������֤������һ�����Ӽ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
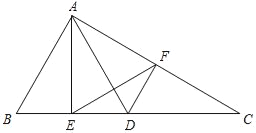
����Ŀ����ͼ���ڡ�ABC�У���DΪ��BC��һ�㣬��AD��AB��AE��BC������Ϊ��E������D��DF��AB������AC�ڵ�F������EF��EF2��![]() BDEC��
BDEC��
(1)��֤����EDF�ס�EFC��
(2)���![]() ����֤��AB��BD��
����֤��AB��BD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ����
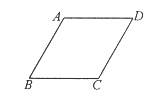
����![]() ����������ڲ�����ϵ�һ�㣬���Ե�
����������ڲ�����ϵ�һ�㣬���Ե�![]() ��
��![]() ��
��![]() Ϊ������������ǵ��������Σ���
Ϊ������������ǵ��������Σ���![]() ��
��![]() ��
��![]() ��
��![]() ���㲻�غϣ���������̾���Ϊ�� ��
���㲻�غϣ���������̾���Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ҽ������ֲ��շѱ�Ϊ180Ԫ/�Σ��������Ա�꿨�������������Żݣ�
��Ա�꿨���� | �쿨���ã�Ԫ�� | ÿ���շѣ�Ԫ�� |
A�� | 1500 | 100 |
B�� | 3000 | 60 |
C�� | 4000 | 40 |
���磬����A���Ա�꿨��һ���ڽ���20�Σ�����![]() Ԫ����һ�����ڸý������ֲ������Ĵ�������50-60��֮�䣬����ʡǮ�ķ�ʽΪ�� ��
Ԫ����һ�����ڸý������ֲ������Ĵ�������50-60��֮�䣬����ʡǮ�ķ�ʽΪ�� ��
A.����A���Ա�꿨B.����B���Ա�꿨
C.����C���Ա�꿨D.�������Ա�꿨
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
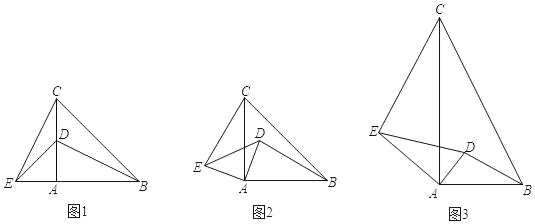
�����龳����ͼ1������ѧ����ϣ���ʦ��ͬѧ�ǻ��˵���Rt��ABC�͵���Rt��ADE��������CE��BD��
�������֣���1��������Rt��ADE�Ƶ�A��ת����ͼ2���ڷ�С�鷢���ˣ�
���߶�CE���߶�BD֮���������ϵ���� ����
��ֱ��CE��ֱ��BD֮���λ�ù�ϵ���� ����
���˼������2���ǻ�С���ڴ˻����Ͻ���������˼������ͼ3������ABC����ADE��Ϊֱ�������Σ���BAC����DAE��90������AC��2AB��AE��2AD������д��CE��BD��������ϵ��λ�ù�ϵ��������֤����
��չӦ�ã���3������С���ڣ�2���Ļ����ϣ������˽�һ����չ�о�������E��ֱ��AB�Ϸ�ʱ����DE��AB����AB��![]() ��AD��1�������������䣬������߶�CE�ij�����ֱ��д�����ۣ�
��AD��1�������������䣬������߶�CE�ij�����ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
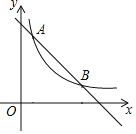
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����kx+m��˫����y��![]() ��x��0������A��B���㣬��A�ĺ�����Ϊ1����B��������Ϊ2����P��y����һ���㣬����PAB���ܳ���Сʱ����P��������_______��
��x��0������A��B���㣬��A�ĺ�����Ϊ1����B��������Ϊ2����P��y����һ���㣬����PAB���ܳ���Сʱ����P��������_______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com