
已知抛物线y=ax2+x+2.
1.当a=-1时,求此抛物线的顶点坐标和对称轴
2.若代数式-x2+x+2的值为正整数,求x的值;
3.若a是负数时,当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0). 若点M在点N的左边,试比较a1与a2的大小.
1.当a=-1时,y=-x2+x+2,∴a=-1,b=1,c=2.
∴抛物线的顶点坐标为(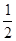 ,
,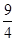 ),对称轴为直线x=
),对称轴为直线x=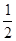 .……2分
.……2分
2.∵代数式-x2+x+2的值为正整数,∴函数y=-x2+x+2的值为正整数.
又因为函数的最大值为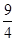 ,∴y的正整数值只能为1或2.
,∴y的正整数值只能为1或2.
当y=1时,-x2+x+2=1,解得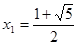 ,
,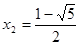 …………3分
…………3分
当y=2时,-x2+x+2=2,解得x3=0,x4=1.……………4分
∴x的值为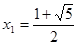 ,
,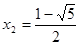 ,0或1.
,0或1.
3.当a<0时,即a1<0,a2<0.
经过点M的抛物线y=a1x2+x+2的对称轴为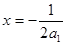 ,
,
经过点N的抛物线y=a2x2+x+2的对称轴为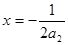 .…………5分
.…………5分

∵点M在点N的左边,且抛物线经过点(0,2)
∴直线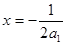 在直线
在直线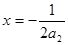 的左侧……………6分
的左侧……………6分
∴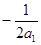 <
<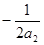 .
.
∴a1<a2.…………………………………………………………7分
【解析】(1)根据二次函数的顶点坐标和对称轴公式求解。
(2)根据函数最大值求得x的值。


科目:初中数学 来源: 题型:
已知抛物线y=ax2+bx+c(a>0)经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式.
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若![]() 存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
标;若存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.查看答案和解析>>
科目:初中数学 来源:2012届山东邹城北宿中学九年级3月月考数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2010-2011年浙江省嵊州市九年级上学期期末考试数学卷 题型:解答题
(本小题满分14分)
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题:

1.(1)求抛物线的解析式和D点的坐标;
2.(2)过点D作DF∥ 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
3.(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com