
 某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).
某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).分析 (1)根据四级台阶高度相等,即可求得答案;
(2)连接CD,可证明四边形ABCD为平行四边形,从而可得到AB∥CD且AB=CD,然后利用锐角三角函数的定义求得CD的长即可得出问题的答案.
解答 解:(1)DH=1.6×$\frac{3}{4}$=1.2米
(2)连接CD.
∵AD∥BC,
∴四边形ABCD为平行四边形.
∴AB∥CD且AB=CD.
∴∠HDC=∠DAB=66.5°
Rt△HDC中,cos∠HDC=$\frac{DH}{CD}$,
∴CD=$\frac{HD}{cos66.5°}≈\frac{1.2}{0.4}$=3(米).
∴l=AD+AB+BC=0.8+3+0.8=4.6(米).
∴所用不锈钢材料的长度约为4.6米.
点评 本题主要考查的是解直角三角形和平行四边形的性质和判定,掌握锐角三角函数的定义是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
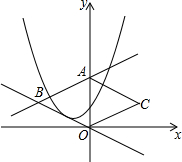 如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,
如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明妈妈买了一部29寸的电视机,小明量了电视机的屏幕后,发现屏幕只有58cm长和46cm宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?
小明妈妈买了一部29寸的电视机,小明量了电视机的屏幕后,发现屏幕只有58cm长和46cm宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+x>b+x | B. | -a+1<-b+1 | C. | 2a<2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
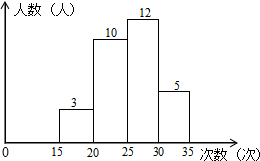 某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1.
某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50cm,EF=25cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB=6.6m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com