
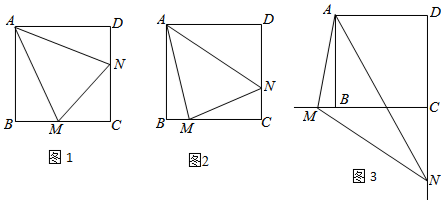
���� ��1������AC����MN�ڵ�G�����֪AC��ֱƽ��MN����ϡ�MAN=45�㣬��֤����ABM�ա�AGM���ɵõ�BM=MG��ͬ���ɵõ�NG=DN���ɵó����ۣ�
��2����MB���ӳ����ϣ���ȡBE=DN������AE�����֤����ABE�ա�ADN���ɵõ�AE=AN����һ����֤����AEM�ա�ANM���ɵý���BM+DN=MN��
��3����DC�Ͻ�ȡDF=BM������AF������֤����ABM�ա�ADF����һ����֤����MAN�ա�FAN���ɵõ�MN=NF���Ӷ��ɵõ�DN-BM=MN
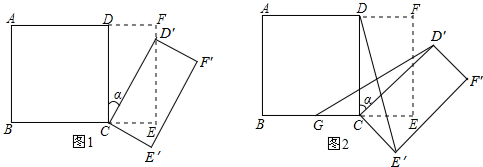
��� �⣺��1����ͼ1������AC����MN�ڵ�G��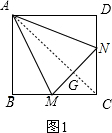
���ı���ABCDΪ�����Σ�
��BC=CD����BM=DN��
��CM=CN����ACƽ�֡�BCD��
��AC��MN����MG=GN��
���MAG=��NAG��
�ߡ�BAC=��MAN=45�㣬����BAM+��GAM=��GAM+��GAN��
���BAM=��GAN=��GAM��
�ڡ�ABM�͡�AGM�У�$\left\{\begin{array}{l}{��B=��AGM=90��}\\{��BAM=��GAM}\\{AM=AM}\end{array}\right.$
���ABM�ա�AGM��AAS����
��BM=MG��ͬ���ɵ�GN=DN��
��BM+DN=MG+GN=MN��
��BM+DN=MN��
��2�����룺BM+DN=MN��
֤�����£�
��ͼ2����MB���ӳ����ϣ���ȡBE=DN������AE��
�ڡ�ABE�͡�ADN�У�$\left\{\begin{array}{l}{AB=AD}\\{��ABE=��D}\\{BE=DN}\end{array}\right.$
���ABE�ա�ADN��SAS����
��AE=AN����EAB=��NAD��
�ߡ�BAD=90�㣬��MAN=45�㣬
���BAM+��DAN=45�㣬
���EAB+��BAM=45�㣬
���EAM=��NAM��
�ڡ�AEM�͡�ANM��$\left\{\begin{array}{l}{AE=AN}\\{��EAM=��NAM}\\{AM=AM}\end{array}\right.$
���AEM�ա�ANM��SAS����
��ME=MN��
��ME=BE+BM=BM+DN��
��BM+DN=MN��
��3��DN-BM=MN��
֤�����£�
��ͼ3����DC�Ͻ�ȡDF=BM������AF��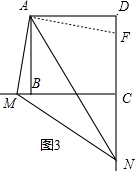
��ABM�͡�ADF�У�$\left\{\begin{array}{l}{AB=AD}\\{��ABM=��D}\\{BM=DF}\end{array}\right.$��
���ABM�ա�ADF��SAS����
��AM=AF����BAM=��DAF��
���BAM+��BAF=��BAF+��DAF=90�㣬��MAF=��BAD=90�㣬
�ߡ�MAN=45�㣬
���MAN=��FAN=45�㣬
�ڡ�MAN�͡�FAN�У�$\left\{\begin{array}{l}{AM=AF}\\{��MAN=��FAN}\\{AN=AN}\end{array}\right.$
���MAN�ա�FAN��SAS����
��MN=NF��
��MN=DN-DF=DN-BM��
��DN-BM=MN��
���� ����Ϊ�ı��ε��ۺ��⣬�漰֪ʶ���������ε����ʡ�ȫ�������ε��ж������ʡ���ֱƽ���ߵ��ж������ʵȣ��ڣ�1����֤��AM=AN�ǽ���Ĺؼ����ڣ�2������3���й���������ȫ���ǽ���Ĺؼ������⿼��֪ʶ�㲻�࣬��������ȫ�ȵĹ����ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
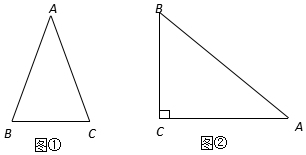 ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA=$\frac{�ױ�}{��}=\frac{BC}{AB}$������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺
ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA=$\frac{�ױ�}{��}=\frac{BC}{AB}$������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
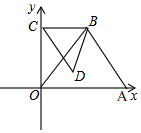 ��ͼ��ֱ������ϵ�У�OΪԭ�㣬A��6��0�����ڵ���������ABO�У�OB=BA=5����B�ڵ�һ���ޣ�C��0��k��Ϊy����������һ���㣬���ԡ�CBDΪ���ǵĵ���������CBD���ҡ�CBD=��OBA������AD��
��ͼ��ֱ������ϵ�У�OΪԭ�㣬A��6��0�����ڵ���������ABO�У�OB=BA=5����B�ڵ�һ���ޣ�C��0��k��Ϊy����������һ���㣬���ԡ�CBDΪ���ǵĵ���������CBD���ҡ�CBD=��OBA������AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
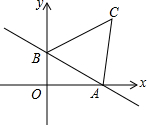 һ�κ���y=-$\frac{{\sqrt{3}}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B����ABΪ���ڵ�һ���������ȱߡ�ABC
һ�κ���y=-$\frac{{\sqrt{3}}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B����ABΪ���ڵ�һ���������ȱߡ�ABC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
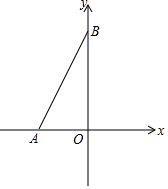 ��ƽ��ֱ������ϵ�У�A��a��0����B��0��b������a��b�Ƕ�Ԫһ�η�����$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$�Ľ⣮
��ƽ��ֱ������ϵ�У�A��a��0����B��0��b������a��b�Ƕ�Ԫһ�η�����$\left\{\begin{array}{l}{a+b-4=0}\\{\frac{1}{2}a-2b+13=0}\end{array}\right.$�Ľ⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com