
【题目】已知A1,A2,A3是抛物线y=![]() x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CA=CB,点O在△ABC的内部,⊙O经过B,C两点,交AB于点D,连接CO并延长交AB于点G,以GD,GC为邻边作GDEC.
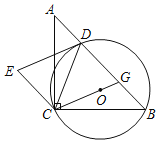
(1)判断DE与⊙O的位置关系,并说明理由.
(2)若点B是![]() 的中点,⊙O的半径为2,求
的中点,⊙O的半径为2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点![]() 的正前方
的正前方![]() 处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为
处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为![]() 时达到最高点,此时足球飞行的水平距离为
时达到最高点,此时足球飞行的水平距离为![]() .已知球门的横梁高
.已知球门的横梁高![]() 为
为![]() .
.
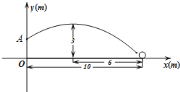
![]() 在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
![]() 守门员乙站在距离球门
守门员乙站在距离球门![]() 处,他跳起时手的最大摸高为
处,他跳起时手的最大摸高为![]() ,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c和一次函数g(x)=﹣bx,其中a、b、c,满足a>b>c,a+b+c=0.
(1)求证:这两个函数的图象交于不同的两点;
(2)设这两个函数的图象交于A,B两点,作AA1⊥x轴于A1,BB1⊥x轴于B1,求线段A1B1的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
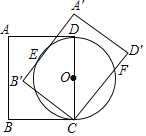
【题目】如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
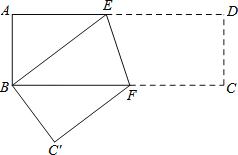
【题目】如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com