
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
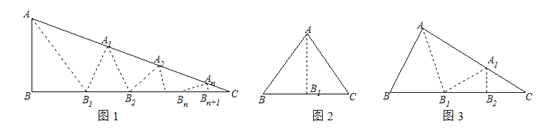
(1)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.
(2)根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 ;
(3)如果一个三角形的最小角是15°,且满足该三角形的三个角均是此三角形的好角,则此三角形另两个角的度数为 .
【答案】(1)∠B=3∠C;(2)∠B=n∠C;(3)15°,150°.
【解析】试题分析:(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的![]() 由
由![]() 又
又![]()
![]() 由此即可求得结果;
由此即可求得结果;
(3)因为最小角是15°是△ABC的好角,根据好角定义,则可设另两角分别为![]() (其中
(其中![]() 都是正整数),由题意得
都是正整数),由题意得![]() 所以
所以![]() 再根据
再根据![]() 都是正整数可得
都是正整数可得 ![]() 与
与![]() 是
是![]() 的整数因子,从而可以求得结果
的整数因子,从而可以求得结果
试题解析:(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是△ABC的好角;
理由如下:小丽展示的情形二中,
∵沿∠BAC的平分线![]() 折叠,
折叠,
∴![]()
又∵将余下部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点C重合,
与点C重合,
∴![]()
∵![]() (外角定理),
(外角定理),
∴∠B=2∠C;
故答案是:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分线![]() 折叠,剪掉重复部分;将余下部分沿
折叠,剪掉重复部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,将余下部分沿
折叠,剪掉重复部分,将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点C重合,则∠BAC是△ABC的好角.
与点C重合,则∠BAC是△ABC的好角.
证明如下:∵根据折叠的性质知, ![]()
∴根据三角形的外角定理知, ![]()
∵根据四边形的外角定理知, ![]()
根据三角形ABC的内角和定理知, ![]()
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
故答案为:∠B=3∠C;∠B=n∠C
(3)由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因为最小角是![]() 是△ABC的好角,
是△ABC的好角,
根据好角定义,则可设另两角分别为![]() (其中m、n都是正整数).
(其中m、n都是正整数).
由题意,得![]() 所以m(n+1)=11
所以m(n+1)=11
因为m、n都是正整数,所以m与n+1是![]() 的整数因子,
的整数因子,
因此有: ![]()
所以m=1,n=10.
所以![]()
所以该三角形的另外两个角的度数分别为:15°,150°.


科目:初中数学 来源: 题型:
【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
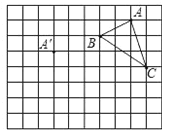
(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的![]() 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
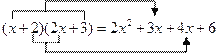
也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
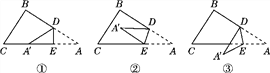
【题目】△ABC是一个三角形的纸片,点D,E分别是△ABC边AB,AC上的两点.
(1)如图①,如果沿直线DE折叠,则∠BDA′与∠A的关系是____________;
(2)如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由;
(3)如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
解答“已知![]() ,且
,且![]() ,
,![]() ,确定
,确定![]() 的取值范围”有如下解,
的取值范围”有如下解,
解:∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,![]() ①
①
同理得:![]() .
.![]() ②
②
由①![]() ②得
②得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
请按照上述方法,完成下列问题:
(![]() )已知
)已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )已知
)已知![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 得取值范围(结果用含
得取值范围(结果用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
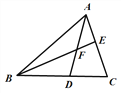
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com