
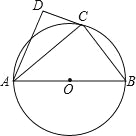
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
【答案】(1) AC=4;(2)详见解析.
【解析】
试题分析:(1)首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;(2)连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.
试题解析:(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4;
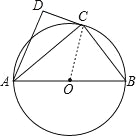
(2)证明:连接OC
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】若A(-3,2)关于原点对称的点是B,B关于y轴对称的点是C,则点C的坐标是( )
A. (3,2) B. (-3,-2)
C. (3,-2) D. (-2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个完全相同的正四面体骰子的各面上分别标明数字1,2,3,4,在桌子上同时投掷这两个正四面体骰子,请用列表法或画树状图的方法,求与桌面接触的面所得的点数之和等于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中的篮球队球员中,一、二年级的成员共有8人,三年级的成员有3人,一、二年级的成员身高(单位:公分)如下:
172,172,174,174,176,176,178,178
若队中所有成员的平均身高为178公分,则队中三年级成员的平均身高为几公分( )
A.178
B.181
C.183
D.186
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm![]() ?
?
(2)△PAQ的面积能否达到3 cm![]() ?
?
(3)经过多长时间,P、Q两点之间的距离为![]() cm?
cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)某百货大搂服装柜在销售中发现:“七彩”牌童装平均每天可售出20件,每件盈利40元.为了迎接“元旦”,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.
(1)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
(2)用配方法说明:要想盈利最多,每件童装应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com