
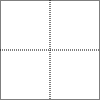
 如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出8条长度为$\sqrt{5}$的线段.
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出8条长度为$\sqrt{5}$的线段.  名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
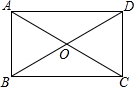 如图,在四边形ABCD中,点O是AC的中点,
如图,在四边形ABCD中,点O是AC的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
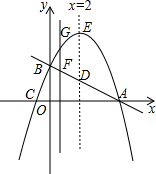 如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.
如图,已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点,抛物线y=-x2+bx+c与x轴交于A、C两点,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
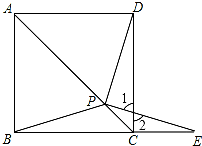 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
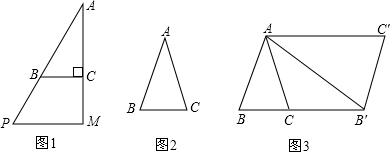
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 18000元 |
| 第二周 | 4台 | 10台 | 31000元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com