Question

5．正方形ABCD的边长为4$\sqrt{2}$，M为BC的中点，以MC为边在正方形ABCD内部作正方形CMNE（如图1），将正方形CMNE绕C点顺时针旋转α（0°≤α≤360°），连接BM、DE．

（1）如图2，试判断BM、DE的关系，并证明；
（2）连接BE，在正方形CMNE绕C点顺时针旋转过程中，若M点在直线BE上时，求BM的长．
（3）如图3，设直线BM与直线DE的交点为P，当正方形CMNE从图1的位置开始，顺时针旋转180°后，直接写出P点运动路径长为$\frac{8}{3}π$．

Answer 1

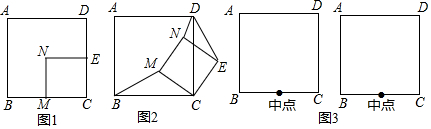
分析 （1）根据正方形的性质以及旋转的性质，判定△BCM≌△DCE（SAS），得出∴BM=DE，再延长BM交DE于F，交DC于G，根据三角形内角和的定理以及对顶角相等，得出BM⊥DE即可；
（2）在正方形CMNE绕C点顺时针旋转过程中，若M点在直线BE上时，需要分两种情况进行讨论，运用勾股定理求得NE和BH的长，进而得到BM的长；
（3）当正方形CMNE旋转到点B、M、N在一条直线上时，点P到达最高点，连结CN，NN'，CN'，根据△CN'N是等边三角形，求得弧CP的长；再根据当正方形CMNE从图4所示的位置，继续顺时针旋转180°后，直线BM与直线DE的交点P从图4所示的位置回到点C与点C重合，据此得出P点运动路径长．

解答 解：（1）BM=DE，BM⊥DE．
理由：∵正方形CMNE绕C点顺时针旋转α，
∴∠MCB=∠ECD=α，CM=CE．
∵ABCD是正方形，
∴BC=CD．
在△BCM和△DCE中，
$\left\{\begin{array}{l}{CB=CD}\\{∠BCM=∠DCE}\\{CM=CE}\end{array}\right.$，
∴△BCM≌△DCE（SAS），
∴BM=DE，
如图，延长BM交DE于F，交DC于G，

∵△BCM≌△DCE，
∴∠CBM=∠CDE，
又∵∠BGC=∠DGF，
∴∠BCG=∠DFG，
∵BC⊥CD，
∴BM⊥DE；

（2）情况①，如图，过点C作CH⊥BE于点H．

∵正方形ABCD的边长为4$\sqrt{2}$，
∴CM=CE=2$\sqrt{2}$．
∴在Rt△MCE中，由勾股定理，得ME=$\sqrt{M{C}^{2}+E{C}^{2}}$=4，
∴MH=EH=2，
∴CH=2．
在Rt△BHC中，BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=2$\sqrt{7}$，
∴BM=2$\sqrt{7}$-2；

情况②，如图，过点C作CH⊥BE'于点H．

∵正方形ABCD的边长为4$\sqrt{2}$，
∴CM=CE=2$\sqrt{2}$．
∴在Rt△MCE中，由勾股定理得ME=4，
∴MH=EH=2，
∴CH=2．
在Rt△BHC中，BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=2$\sqrt{7}$，
∴BM=2$\sqrt{7}$+2；

（3）如图，当正方形CMNE旋转到点B、M、N在一条直线上时，点P到达最高点，连结CN，NN'，CN'．

∵正方形ABCD的边长为4$\sqrt{2}$，M为BC的中点，
∴CM'=CM=2$\sqrt{2}$．
∴∠M'BC=30°，
∴∠BCM'=60°，
由旋转得∠NCN'=60°，NC=N'C，
∴△CN'N是等边三角形，
∴∠CNN'=60°，
∴弧CP的长为$\frac{60×π×4}{180}$=$\frac{4}{3}π$，
如图，当正方形CMNE从图4所示的位置，继续顺时针旋转180°后，直线BM与直线DE的交点P从图4所示的位置回到点C的位置，

∴点P的运动路径长为$\frac{4}{3}π$×2=$\frac{8}{3}π$．
故答案为$\frac{8}{3}π$．

点评 本题属于四边形综合题，主要考查了正方形的性质，勾股定理以及旋转的性质的综合应用，解决问题的关键是画出图形，作辅助线构造直角三角形，结合勾股定理进行计算求解．解题时注意分类讨论思想的运用．