
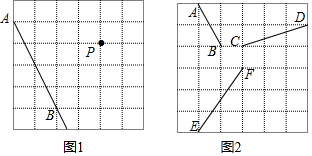
分析 (1)根据网格结构的特点,利用直线与网格的夹角的关系找出与AB平行的格点以及垂直的格点作出即可;
(2)根据网格结构的特点,过点E找出与AB、CD位置相同的线段,过点F找出与AB、CD位置相同的线段,作出即可;
(3)根据S△=S正方形-三个角上的三角形的面积即可得出结论.
解答 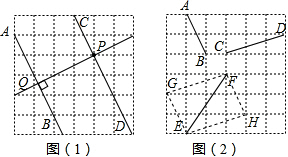 解:(1)、(2)如图所示;
解:(1)、(2)如图所示;
(3)S△EFH=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×3
=9-1-3-$\frac{3}{2}$
=3.5.
故答案为:3.5.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.


科目:初中数学 来源: 题型:解答题
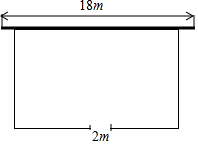 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系xOy中,二次函数y=ax2的图象经过点A、B、O,则下列对二次项系数a判断正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2的图象经过点A、B、O,则下列对二次项系数a判断正确的是( )| A. | a>0 | B. | a=0 | C. | a<0 | D. | a≥0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com