
分析 (1)根据已知等式得出规律,写出所求结果即可;
(2)利用二次根式性质计算得到结果即可;
(3)归纳总结得到一般性规律,写出即可.
解答 解:(1)根据题意得:$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$;$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$;
故答案为:5$\sqrt{\frac{1}{6}}$;6$\sqrt{\frac{1}{7}}$;
(2)$\sqrt{2014+\frac{1}{2016}}$=$\sqrt{\frac{2014×2016+1}{2016}}$=$\sqrt{\frac{(2015+1)×(2015-1)+1}{2016}}$=$\sqrt{\frac{201{5}^{2}-1+1}{2016}}$=2015$\sqrt{\frac{1}{2016}}$;
(3)归纳总结得:$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(自然数n≥1).
点评 此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒钟后△DPQ的面积等于28cm2?
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒钟后△DPQ的面积等于28cm2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年9月8日,湖南省水利厅在长沙召开全省农田灌溉水测算工作布置和实测座谈会,该会议就农田灌溉水的实测技术进行了讲授与答疑.如图,某村有A,B两区城的农田,MN是一条河流,为方便农田灌溉,要铺设管道将河水引到A,B两个用水点,现有下列两种铺设方案,请你判断这两种方案中,哪一种比较节省材料?并说明理由.
2015年9月8日,湖南省水利厅在长沙召开全省农田灌溉水测算工作布置和实测座谈会,该会议就农田灌溉水的实测技术进行了讲授与答疑.如图,某村有A,B两区城的农田,MN是一条河流,为方便农田灌溉,要铺设管道将河水引到A,B两个用水点,现有下列两种铺设方案,请你判断这两种方案中,哪一种比较节省材料?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
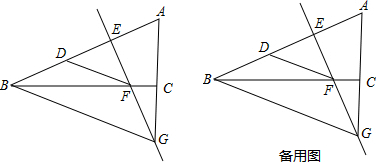
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com