
【题目】已知ai≠0(i=1,2,…,2012)满足 ![]() ,使直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限的ai概率是 .
,使直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限的ai概率是 .
【答案】![]()
【解析】解:∵ai≠0(i=1,2,…,2012)满足 ![]() ,∴(2012﹣1968)÷2=22,2012﹣22=1990,
,∴(2012﹣1968)÷2=22,2012﹣22=1990,
∴ai有22个是负数,1990个是正数,
∵ai<0时直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限,
∴使直线y=aix+i(i=1,2,…,2012)的图象经过一、二、四象限的ai概率是 ![]() =
= ![]() ,
,
所以答案是: ![]() ,
,
【考点精析】关于本题考查的绝对值和概率公式,需要了解正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】给出定义:设一条直线与一条抛物线只有一个公共点,且这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题: ①直线y=0是抛物线y= ![]() x2的切线;
x2的切线;
②直线x=﹣2与抛物线y= ![]() x2 相切于点(﹣2,1);
x2 相切于点(﹣2,1);
③若直线y=x+b与抛物线y= ![]() x2相切,则相切于点(2,1);
x2相切,则相切于点(2,1);
④若直线y=kx﹣2与抛物线y= ![]() x2相切,则实数k=
x2相切,则实数k= ![]() .
.
其中正确命题的是( )
A.①②④
B.①③
C.②③
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克B.3.7×10﹣6克C.37×10﹣7克D.3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.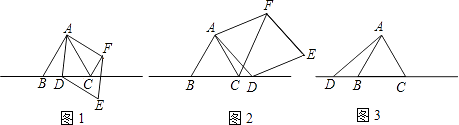
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则P′A:PB=( ) 
A.1: ![]()
B.1:2
C.![]() :2
:2
D.1: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com