
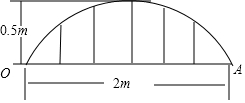
 某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.分析 (1)根据所建坐标系特点可设解析式为y=ax2+c的形式,结合图象易求B点和C点坐标,代入解析式解方程组求出a,c的值得解析式;
(2)根据对称性求B3、B4的纵坐标后再求出总长度.
解答 解:(1)由题意得B(0,0.5)、C(1,0)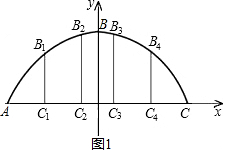
设抛物线的解析式为:y=ax2+c
代入得a=-0.5,c=0.5,
故解析式为y=-0.5x2+0.5;
(2)如图1所示:
∵当x=0.2时,y=0.48,
当x=0.6时,y=0.32,
∴B1C1+B2C2+B3C3+B4C4=2×(0.48+0.32)=1.6米
∴所需不锈钢管的总长度为:1.6×50=80米.
点评 本题考查了二次函数的应用,利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
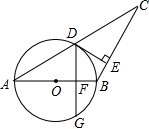 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.
如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
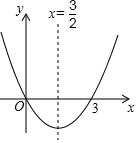 如图所示的二次函数图象上有3个点(-3,y1),(m,y2),(2,y3),若y1>y2>y3,则m可以取得的最大整数值为( )
如图所示的二次函数图象上有3个点(-3,y1),(m,y2),(2,y3),若y1>y2>y3,则m可以取得的最大整数值为( )| A. | -1 | B. | 5 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com