
【题目】如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
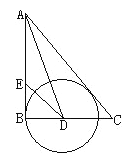
求证:(1)AC是⊙D的切线;(2)AB+EB=AC.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】试题(1)过点D作DF⊥AC于F,求出BD=DF等于半径,得出AC是⊙D的切线.
(2)先证明△BDE≌△FCD(HL),根据全等三角形对应边相等及切线的性质的AB=AF,得出AB+EB=AC.
证明:(1)过点D作DF⊥AC于F;(1分)
∵AB为⊙D的切线,AD平分∠BAC,
∴BD=DF,(3分)
∴AC为⊙D的切线.(4分)
(2)∵AC为⊙D的切线,
∴∠DFC=∠B=90°,
在Rt△BDE和Rt△FCD中;
∵BD=DF,DE=DC,
∴Rt△BDE≌Rt△FCD(HL),(6分)
∴EB=FC.(8分)
∵AB=AF,
∴AB+EB=AF+FC,
即AB+EB=AC.(10分)


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
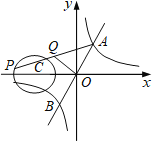
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
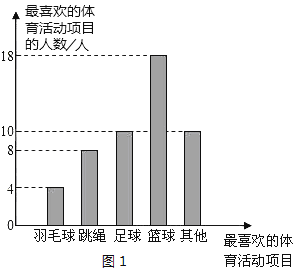
【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A,B两点的切线交于点C,测得∠C=120°,A,B两点之间的距离为60m,则这段公路AB的长度是( )
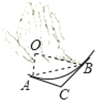
A.10πmB.20πmC.10![]() πmD.60m
πmD.60m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2﹣2x﹣3,一次函数y2=x﹣1.
(1)在同一坐标系中,画出这两个函数的图象;
(2)根据图形,求满足y1>y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
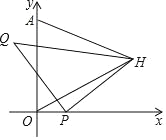
【题目】如图,在平面直角坐标系中,已知Q(﹣1,3),A(0,4),点P为x轴上一动点,以QP为腰作等腰Rt△QPH,当OH+AH最小时,点H的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,同学们利用所学知识去测量海平面上一个浮标到海岸线的距离. 在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,小宇同学在A处观测得浮标在北偏西60°的方向,小英同学在距点A处60米远的B点测得浮标在北偏西45°的方向,求浮标C到海岸线l的距离(结果精确到0.01 m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知公路L上A,B两点之间的距离为100米,小明要测量点C与河对岸的公路L的距离,在A处测得点C在北偏东60°方向,在B处测得点C在北偏东30°方向,则点C到公路L的距离CD为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com