练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.

    已知：直线和直线外一点.

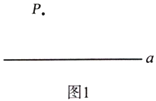
    求作：直线的垂线，使它经过.

    作法：如图2.

    （1）在直线上取一点，连接；

    （2）分别以点和点为圆心，大于的长为半径作弧，两弧相交于，两点，连接交于点；

    （3）以点为圆心，为半径作圆，交直线于点（异于点），作直线.所以直线就是所求作的垂线.

    请你写出上述作垂线的依据：______.

    【答案】直径所对的圆周角是直角

    【解析】

    由题意知点E在以PA为直径的圆上，根据“直径所对的圆周角是直角”可得∠PEA＝90°，即PE⊥直线a．

    由作图知，点E在以PA为直径的圆上，

    所以∠PEA＝90°，

    则PE⊥直线a，

    所以该尺规作图的依据是：直径所对的圆周角是直角，

    故答案为：直径所对的圆周角是直角．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

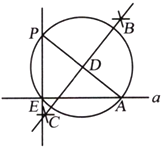
    【题目】下面是小华同学设计的“作三角形的高线”的尺规作图的过程．

    已知：如图1，△ABC．

    求作：AB边上的高线．

    作法：如图2，

    ①分别以A，C为圆心，大于长

    为半径作弧，两弧分别交于点D，E；

    ② 作直线DE，交AC于点F；

    ③ 以点F为圆心，FA长为半径作圆，交AB的延长线于点M；

    ④ 连接CM．

    则CM 为所求AB边上的高线．

    根据上述作图过程，回答问题：

    （1）用直尺和圆规，补全图2中的图形；

    （2）完成下面的证明：

    证明：连接DA，DC，EA，EC，

    ∵由作图可知DA=DC =EA=EC，

    ∴DE是线段AC的垂直平分线．

    ∴FA=FC ．

    ∴AC是⊙F的直径．

    ∴∠AMC=______°（___________________________________）（填依据），

    ∴CM⊥AB．

    即CM就是AB边上的高线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九年级（1）班的小华和小红两名学生10次数学测试成绩如下表（表I）所示：

    小花

    70

    80

    90

    80

    70

    90

    80

    100

    60

    80

    小红

    90

    80

    100

    60

    90

    80

    90

    60

    60

    90

    现根据上表数据进行统计得到下表（表Ⅱ）：

    姓名

    平均成绩

    中位数

    众数

    小华

    80

    小红

    80

    90

    （1）填空：根据表I的数据完成表Ⅱ中所缺的数据；

    （2）老师计算了小红的方差请你计算小华的方差并说明哪名学生的成绩较为稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 已知于x的元二次方程x2﹣6x+2a+5＝0有两个不相等的实数根x1，x2．

    （1）求a的取值范围；

    （2）若x12+x22﹣x1x2≤30，且a为整数，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某玩具商店以每件60元为成本购进一批新型玩具，以每件100元的价格销售则每天可卖出20件，为了扩大销售，增加盈利，尽快减少库存，商店决定采取适当的降价措施，经调查发现：若每件玩具每降价1元，则每天可多卖2件.

    (1)若商店打算每天盈利1200元，每件玩具的售价应定为多少元？

    (2)若商店为追求效益最大化，每件玩具的售价定为多少元时，商店每天盈利最多？最多盈利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，的直径，点为线段上一动点，过点作的垂线交于点，，连结，.设的长为，的面积为.

    小东根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究.

    下面是小东的探究过程，请帮助小东完成下面的问题.

    （1）通过对图1的研究、分析与计算，得到了与的几组对应值，如下表：

    0

    0.5

    1

    1.5

    2

    2.5

    3

    3.5

    4

    0

    0.7

    1.7

    2.9

    4.8

    5.2

    4.6

    0

    请求出表中小东漏填的数；

    （2）如图2，建立平面直角坐标系，描出表中各对应值为坐标的点，画出该函数的大致图象；

    （3）结合画出的函数图象，当的面积为时，求出的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学课外活动小组的同学．利用所学的数学知识，测底部可以到达的学校操场上的旗杆AB高度，他们采用了如下两种方法：

    方法1：在地面上选一点C，测得CB为40米，用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°；

    方法2：在相同时刻测得旗杆AB的影长为17.15米，又测得已有的2米高的竹杆的影长为1.5米．

    你认为这两种方法可行吗？若可行，请你任选一种方法算出旗杆高度（精确到0.1米）若不可行，自己另设计一种测量方法（旗杆顶端不能到达），算出旗杆高度（结果可用字母表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AB是直径，OD⊥AC，垂足为D点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PB，PC，且满足∠PCA＝∠ABC

    （1）求证：PA＝PC；

    （2）求证：PA是⊙O的切线；

    （3）若BC＝8，，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了提高学生的综合素质，成立了以下社团：．机器人，．围棋，．羽毛球，．电影配音．每人只能加入一个社团．为了解学生参加社团的情况，从加社团的学生中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图，其中图中所占扇形的圆心角为．

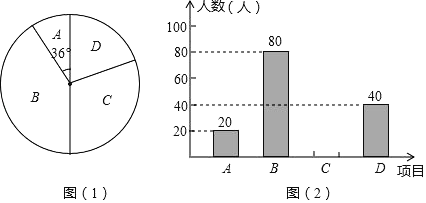
    根据以上信息，解答下列问题：

    这次被调查的学生共有　 　人；

    请你将条形统计图补充完整；

    若该校共有学生加入了社团，请你估计这名学生中有多少人参加了羽毛球社团；

    在机器人社团活动中，由于甲、乙、丙、丁四人平时的表现优秀，现决定从这四人中任选两名参加机器人大赛．用树状图或列表法求恰好选中甲、乙两位同学的概率．

    查看答案和解析>>

    同步练习册答案