
分析 当汽车出现故障时,乘这辆车的3人下车步行,另一辆车将自己车内的4人送到车站再回来接步行的3人再送至火车站,此时可以设出现故障后乘这辆车的3人下车步行的距离为x,根据人走的时间和车返回时接的时间相同,可列出方程,得解后即可得出现故障后先步行的3人到达车站总共的用时;
利用小汽车先送4人到中途某地下车,这4人步行去车站,而同时另外3人先步行,在乘返回的小汽车到车站,并且两批人同时到达火车站,根据人走的时间和车返回时接的时间相同,可列出方程,得解后即可得出现故障后先走的4人到达车站总共的用时.
解答 解:设乘出现故障汽车的3个人步行的距离为x千米,根据题意得,
有,$\frac{x}{4}$=$\frac{10+10-x}{40}$,
解得:x=$\frac{20}{11}$,
这7个人全部到达火车站所需时间
$\frac{20}{11}$÷4+(10-$\frac{20}{11}$)÷40=$\frac{29}{44}$(小时)=39$\frac{6}{11}$(分钟);
当小汽车出现故障时,乘这辆车的3个人下车步行,另一辆车将车内的4个人送到某地方后,让他们下车步行,再立即返回接出故障汽车而步行的另外3个人,使得两批人员最后同时到达车站.两批人员步行的距离相同,如图,D为无故障汽车人员下车地点,C为故障汽车人员再次上车地点.因此,设AC=DB=y,根据题意得,有:$\frac{y}{4}=\frac{10-y+10-2y}{40}$,
解得:y=$\frac{20}{13}$,因此这,7个人同时到达火车站所需时间
为$\frac{20}{13}$÷4+(10-$\frac{20}{13}$)÷40=$\frac{31}{52}$(小时)=35$\frac{10}{13}$(分钟)
因为35$\frac{10}{13}$<39$\frac{6}{11}$<40,
所以这两种方案可行,方案二所用的时间更少.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,设计合适的方案,根据等量关系列出方程,再求解判断方案是否可行.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
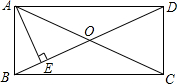 如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )
如图,矩形ABCD中,AE⊥BD垂足为E,若∠DAE=3∠BAE,则∠EAC的度数为( )| A. | 67.5° | B. | 45° | C. | 22.5° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80 | B. | 90 | C. | 85 | D. | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α°(0<α<45°),得到∠B′AD′,其中射线AB′与过点B且与对角线BD垂直的直线交于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,作∠BCM的角平分线交AB于点N,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BN的长度为2$\sqrt{3}$-2.
如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α°(0<α<45°),得到∠B′AD′,其中射线AB′与过点B且与对角线BD垂直的直线交于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,作∠BCM的角平分线交AB于点N,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BN的长度为2$\sqrt{3}$-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com