
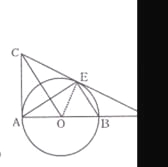
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D, 连接BE,过点O作OC∥BE交切线DE于点C,连接AC .

(1)求证:AC是⊙O的切线 ;
(2)若BD=OB=4,求弦AE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题(1)连结OE,根据条件证明△AOC≌△EOC,进而得出∠CAO=∠CEO =90°即可;(2)利用直角三角形的性质和特殊角的三角函数值,可求出线段AE的长.
试题解析:(1)证明:连结OE,
因为CD与⊙O相切于点E,所以OE![]() CD,所以∠CEO =90°,
CD,所以∠CEO =90°,
因为OC∥BE,所以∠AOC=∠OBE,∠COE=∠OEB,
因为OB=OE,所以∠OBE=∠OEB,所以∠AOC=∠COE,
因为OA=OE,OC=OC, 所以△AOC≌△EOC,
所以∠CAO=∠CEO =90°, 所以AC是⊙O的切线 ;
(2)解:在Rt△DEO中,因为BD=OB, 所以BE=![]() OD=OB=4,
OD=OB=4,
又因为OB=OE, 所以△AOC是等边三角形,所以∠ABE=60°,
因为AB为直径,所以∠AEB=90°,
在Rt△ABE中,AE=tan60°![]() BE=
BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
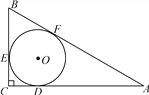
【题目】如图,⊙O为△ABC的内切圆,切点分别为D,E,F,∠C=90°,BC=3,AC=4.
(1)求△ABC的面积;
(2)求⊙O的半径;
(3)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
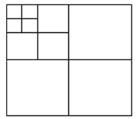
(1)填表
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪n次,共剪出多少个小正方形?
(3)能否经过若干次分割后共得到2019片纸片?若能,请直接写出相应的次数,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
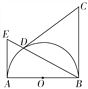
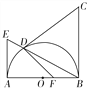
图4① 图4②
(1)如图①,若CD=CB,求证:CD为半圆O的切线;
(2)如图②,若点F在OB上,且FD⊥CD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个水坝的横断面,坝顶宽CD=8米,坝高DE=12米,迎水坡BC的坡比i1=1∶2,背水坡AD的坡比i2=1∶1.
求:(1)∠A的度数;
(2)坝底宽AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,已知某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解下列问题:
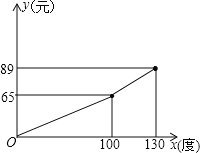
(1)写出y与x的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电60度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com