
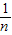 [(x1-
[(x1-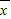 )2+(x2-
)2+(x2-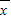 )2+…+(xn-
)2+…+(xn-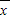 )2],计算出方差,再根据方差的意义可得到答案.
)2],计算出方差,再根据方差的意义可得到答案. 甲=
甲=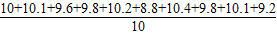 =9.8.
=9.8.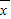 乙
乙 =(9.7+10.1+9.9+10+8.9+9.6+9.6+10.3+10.2+9.7)÷10=9.8;
=(9.7+10.1+9.9+10+8.9+9.6+9.6+10.3+10.2+9.7)÷10=9.8; [(10-9.8)2+(10.1-9.8)2+(9.6-9.8)2+(9.8-9.8)2+(10.2-9.8)2+(8.8-9.8)2
[(10-9.8)2+(10.1-9.8)2+(9.6-9.8)2+(9.8-9.8)2+(10.2-9.8)2+(8.8-9.8)2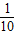 [(9.7-9.8)2+(10.1-9.8)2+(10-9.8)2+(9.9-9.8)2+(8.9-9.8)2+(9.6-9.8)2+(9.6-9.8)2
[(9.7-9.8)2+(10.1-9.8)2+(10-9.8)2+(9.9-9.8)2+(8.9-9.8)2+(9.6-9.8)2+(9.6-9.8)2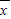 ,则方差S2=
,则方差S2=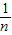 [(x1-
[(x1-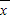 )2+(x2-
)2+(x2-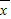 )2+…+(xn-
)2+…+(xn-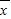 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年山东省青岛市中考数学模拟试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《有理数》(08)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年江苏省苏州市相城区初三第一学期调研测试数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年福建省泉州市德化县初中学业质量检查数学试卷(二)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com