
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价 |
|
|
|
|
数目 |
|
|
|
|
下列说法正确的是( )
A.该班级所售图书的总收入是![]() 元B.在该班级所传图书价格组成的一组数据中,中位数是
元B.在该班级所传图书价格组成的一组数据中,中位数是![]() 元
元
C.在该班级所售图书价格组成的一组数据中,众数是![]() 元D.在该班级所售图书价格组成的一组数据中,平均数是
元D.在该班级所售图书价格组成的一组数据中,平均数是![]() 元
元
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
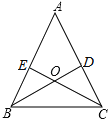
【题目】如图,△ABC的两条高BD、CE相交于点O 且OB=OC.则下列结论:
①△BEC≌△CDB;
②△ABC是等腰三角形;
③AE=AD;
④点O在∠BAC的平分线上,
其中正确的有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某市准备为试点学校采购一批![]() 两种型号的一体机,经过市场调查发现,每套
两种型号的一体机,经过市场调查发现,每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多
型一体机的价格多![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买![]() 套
套![]() 型一体机和
型一体机和![]() 套
套![]() 型一体机.
型一体机.
(1)列二元一次方程组解决问题:求每套![]() 型和
型和![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)由于需要,决定再次采购![]() 型和
型和![]() 型一体机共
型一体机共![]() 套,此时每套
套,此时每套![]() 型体机的价格比原来上涨
型体机的价格比原来上涨![]() ,每套
,每套![]() 型一体机的价格不变.设再次采购
型一体机的价格不变.设再次采购![]() 型一体机
型一体机![]() 套,那么该市至少还需要投入多少万元?
套,那么该市至少还需要投入多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
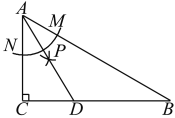
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
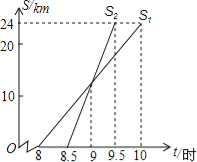
A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读,并完成填空与证明:
初二(8)、(9)班数学兴趣小组展示了他们小组探究发现的结果,内容为:图1,正三角形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,发现利用“
,发现利用“![]() ”证明
”证明![]() ≌
≌![]() ,可得到
,可得到![]() ,
,![]() ,再利用三角形的外角定理,可求得
,再利用三角形的外角定理,可求得![]()
(1)图2正方形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度,请证明你的结论.
度,请证明你的结论.
(2)图3正五边形![]() 中,在
中,在![]() ,
,![]() 边上分别取
边上分别取![]() ,
,![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,那么
,那么![]() ,且
,且![]() 度;
度;
(3)请你大胆猜测在正![]() 边形中的结论:
边形中的结论:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com