已知:关于x的一元二次方程x2-2x+c=0的一个实数根为3.
(1)求c的值;
(2)二次函数y=x2-2x+c,当-2<x≤2时,y的取值范围;
(3)二次函数y=x2-2x+c与x轴交于点A、B(A左B右),顶点为点C,问:是否存在这样的点P,以P为位似中心,将△ABC放大为原来的2倍后得到△DEF(即△EDF∽△ABC,相似比为2),使得点D、E恰好在二次函数上且DE∥AB?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵一元二次方程x
2-2x+c=0的一个实数根为3,
∴3
2-2×3+c=0,
解得c=-3;
(2)二次函数为y=x
2-2x-3=(x-1)
2-4,
x<1时,y随x的增大而减小,
x>1时,y随x的增大而增大,
∵-2<x≤2,
∴当x=-2时,取得最大值为(-2)
2-2×(-2)-3=4+4-3=5,
当x=1时,取得最小值为-4,
∴-2<x≤2时,y的取值范围是-4≤y<5;
(3)存在.
由x
2-2x-3=0得,x
1=-1,x
2=3,
则点A(-1,0),B(3,0),
则AB=3-(-1)=4,
∵△EDF∽△ABC,相似比为2,
∴DE=2×4=8,
∵二次函数为y=x
2-2x-3=(x-1)
2-4的对称轴为直线x=1,
∴点D的横坐标为5或-3,
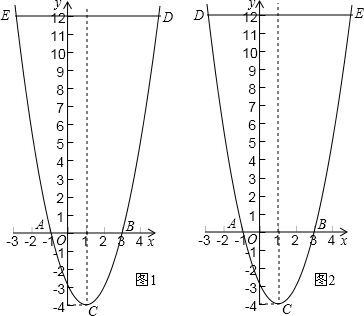
①如图1,点D在点E的右边时,点D的横坐标为5,点E的横坐标为-3,
所以,y=5
2-2×5-3=12,
此时,点D(5,12),E(-3,12),
设直线AE的解析式为y=kx+b,直线BD的解析式为y=ex+f,
则

,
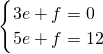
,
解得
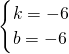
,

,
所以直线AE的解析式为y=-6x+6,
直线BD的解析式为y=6x-18,
联立
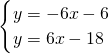
,
解得
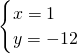
,
所以,点P的坐标为(1,-12),
②如图2,点D在点E的左边时,点E的横坐标为5,点D的横坐标为-3,
所以,y=5
2-2×5-3=12,
此时,点E(5,12),D(-3,12),
设直线AE的解析式为y=kx+b,直线BD的解析式为y=ex+f,
则
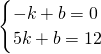
,
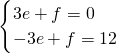
,
解得

,
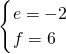
,
所以,直线AE的解析式为y=2x+2,
直线BD的解析式为y=-2x+6,
联立
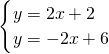
,
解得
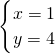
,
所以点P的坐标为(1,4).
综上所述,存在位似中心点P(1,-12)或(1,4).
分析:(1)根据方程根的定义,把实数根3代入方程进行计算即可求出c的值;
(2)把二次函数解析式整理成顶点式形式,然后根据二次函数的增减性求出最大值与最小值,即可得解;
(3)解方程求出点A、B的坐标,然后求出AB的长度,再根据相似比求出DE的长度,然后分:①点D在点E的右边;②点D在点E的左边两种情况,根据二次函数的对称性求出点D的横坐标,然后代入二次函数解析式求出点D的纵坐标,再求出点E的坐标,利用待定系数法求函数解析式求出直线AE、BD的解析式,再根据对应点的连线必过位似中心,联立求解即可得到点P的坐标.
点评:本题考查了二次函数综合题型,主要涉及一元二次方程的解,二次函数的增减性,与x轴的交点问题,位似变换,待定系数法求直线解析式,难度较大,综合性较强,(3)因为点D、E的左右位置不明确,所以要分两种情况讨论求解.


 ,
,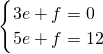 ,
,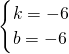 ,
, ,
,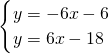 ,
,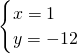 ,
,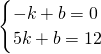 ,
,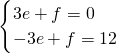 ,
, ,
,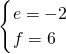 ,
,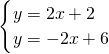 ,
,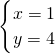 ,
,
