
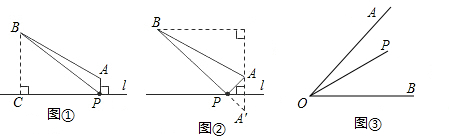
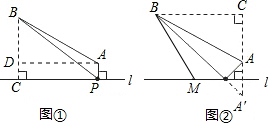
 =40,
=40,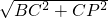 =40
=40 ,
, +10.
+10. =10
=10 ,
, ,
,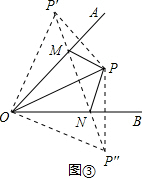
 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
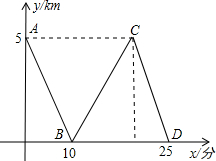 小明家、小亮家、学校在一条直的街道上,平时他俩乘同一校车上学,小明家距学校比小亮家远,每天小明比小亮早5分钟乘上校车上学.某日,因小明比每天晚了5分钟赶不上校车,由爸爸开自家车送小明上学.设两车均匀速行驶,小亮乘车时间为x(分),小明与小亮之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
小明家、小亮家、学校在一条直的街道上,平时他俩乘同一校车上学,小明家距学校比小亮家远,每天小明比小亮早5分钟乘上校车上学.某日,因小明比每天晚了5分钟赶不上校车,由爸爸开自家车送小明上学.设两车均匀速行驶,小亮乘车时间为x(分),小明与小亮之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象解决以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第19-26期 总第175-182期 北师大版 题型:022
在实际问题中,一组数据中各个数据的重要程度未必相同,在计算这组数据的平均数时,往往给每个数据一个“________”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com