
����Ŀ����ͼ����������������A��B��C����ʾ�����ֱ��ǩ�4����2��3����ش�
��1����ʹC��B����ľ�����A��B����ľ�����ȣ����轫��C�����ƶ�_____����λ��
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶����˶�t���ӹ���
����A��B��C��ʾ�����ֱ���_____��_____��_____ ���ú�t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2�����ʣ�d1��d2��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬�����d1��d2ֵ��
![]()
���𰸡� 3��7 ��4��t ��2+2t ��2+2t
�������������������1����AB=2��������ἴ�ɵó���C�����ƶ��ľ��룻
��2���ٽ��·��=ʱ����ٶ�д���𰸣�
�������d1=3t+5��d2=3t+2���Ӷ��ó�d1��d2=2��
�����������1���������֪��A��B����ľ���Ϊ2��B�㡢C���ʾ�����ֱ�Ϊ����2��3��
���Ե�C��B����ľ�����A��B����ľ������ʱ���轫��C�����ƶ�3����7����λ��
�ʴ��ǣ�3��7��
��2���ٵ�A��ʾ�����ǩ�4��t����B��ʾ�����ǩ�2+2t����C����ʾ������3+5t��
�ʴ��ǣ���4��t����2+2t��3+5t��
��d1��d2��ֵ������ʱ��t�ı仯���ı䣬��ֵ��3���������£�
�ߵ�A����ÿ��1����λ���ٶ������˶�����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���
��d1=3t+5��d2=3t+2��
��d1��d2=��3t+5������3t+2��=3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽx3��5xy2��7y3+8x2y��ijһ����ĸ���������У���ȷ���ǣ� ��
A.x3��7y3��5xy2+8x2y
B.��7y3��5xy2+8x2y+x3
C.7y3��5xy2+8x2y+x3
D.x3��5xy2+8x2y��7y3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c�IJ��ֶ�Ӧֵ���±�
x | ��3 | ��2 | ��1 | 0 | 1 | 2 |
y | ��12 | ��5 | 0 | 3 | 4 | 3 |
���ö��κ�����ͼ���֪��������ֵy��0ʱ��x��ȡֵ��Χ�ǣ�������
A.0��x��2B.x��0��x��2C.��1��x��3D.x����1��x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ˮ��������������A�е�һ��ˮ�������������ۣ��л������������䷽ʽ����������е���ľ�Ϊ200Ԫ��ʱ��������Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶȣ�ǧ�ף�ʱ�� | �˷ѣ�Ԫ��ǧ�ף� | װж���ã�Ԫ�� |
�� | 100 | 15 | 2000 |
���� | 80 | 20 | 900 |
(1)�����������֧�����ñȻ��ö�1100Ԫ����֪��������A��֮���·���Ƕ���ǧ���������з��̽����
(2)���A����ij��֮��ľ���ΪSǧ�ף���֪������������·�ϵ����ʱ��ֱ�Ϊ2Сʱ��3.1Сʱ��������ij��ˮ���������ŵľ�����Ҫ������ˮ����A�������������ۡ��㽫ѡ���������䷽ʽ�ȽϺ����أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��BC�ǡ�O��ֱ����A�ǡ�O��һ�㣬����B����O�����ߣ���CA���ӳ����ཻ�ڵ�E��F��BE���е㣬�ӳ�AF��CB���ӳ����ཻ�ڵ�P��
��1����֤��PA�ǡ�O�����ߣ�
��2����ͼ2����AD��BC�ڵ�D������CF��AD�ཻ�ڵ�G����֤��AG=GD��
��3���ڣ�2���������£���FG=BF���ҡ�O�İ뾶��Ϊ![]() ����BD�ij��ȣ�
����BD�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m��n��������������1��n��m�����а���ĸx�Ľ��������ǣ� ��
A.xm+yn��2xy
B.yn+xm��2xy
C.xm��2xy+yn
D.yn��2xy+xm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳���4cm��E��AB���е㣬��DE��AB��������ABCD�����Ϊcm2 �� 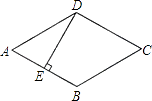
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={x��Z|��x+1����x��4��=0}��B={x|x��a}����A��B=A����a��ֵ�����ǣ� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com