
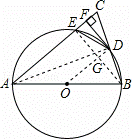
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,与边AC交于点E,过点D作DF⊥AC于F.
(1)求证:DF为⊙O的切线;
(2)若DE=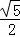 ,AB=
,AB=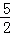 ,求AE的长.
,求AE的长.

(1)证明:连接AD,OD;
∵AB为⊙O的直径,
∴∠ADB=90°,
即AD⊥BC;
∵AB=AC,
∴BD=DC.
∵OA=OB,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD.
∴∠ODF=∠DFA=90°,
∴DF为⊙O的切线.
(2)解:连接BE交OD于G;
∵AC=AB,AD⊥BC,ED=BD,
∴∠EAD=∠BAD.
∴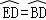 .
.
∴ED=BD,OE=OB.
∴OD垂直平分EB.
∴EG=BG.
又AO=BO,
∴OG= AE.
AE.
在Rt△DGB和Rt△OGB中,
BD2﹣DG2=BO2﹣OG2
∴( )2﹣(
)2﹣(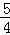 ﹣
﹣ OG)2=BO2﹣OG2
OG)2=BO2﹣OG2
解得:OG= .
.
∴AE=2OG= .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
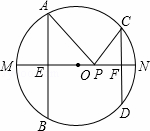
如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD .
.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=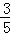 ,求tan∠DBC的值.
,求tan∠DBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
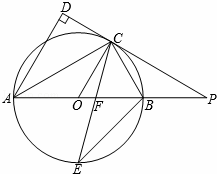
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若tan∠ABC= ,BE=7
,BE=7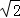 ,求线段PC的长.
,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁.
(Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A′C′的位置时,A′C′的长为 m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com