
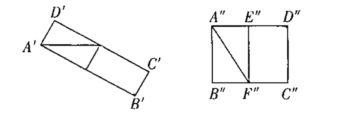
【题目】菱形ABCD中,AB=8,∠B=120°,沿过菱形不同的顶点裁剪两次,再将所裁下的图形拼接,若恰好能无缝,无重叠的拼接成一个矩形,则所得矩形的对角线长为_____.
【答案】![]() 或者
或者![]()
【解析】
按两种情况讨论,根据题意可知两种情况可拼出的新矩形一样,再根据菱形的性质以及矩形的性质,由勾股定理求解即可得到新矩形的对角线的长度;
解:分情况讨论,
情况①,如图,分别沿菱形的对角线AC、BD裁剪,将剪下的四个三角形重新拼接得到矩形![]() 或者矩形
或者矩形![]() ,如图,
,如图,


∵AB=8,∠B=120°,
∴![]() ,
,![]() ,
,
当拼成矩形![]() 时,有
时,有![]() ,
,![]() ,
,
∴矩形对角线长为:![]() ,
,
当拼成矩形![]() 时,有
时,有![]() ,
,![]() ,
,
∴矩形对角线长为:![]() ;
;
情况②,过B作BE⊥AD,过D作DF⊥BC,分别沿BE、DF裁剪,将剪下的三角形和剩余的矩形重新拼接得到和①一样的新矩形![]() 或者矩形
或者矩形![]() ,如图,
,如图,

因此新矩形的对角线长为![]() 或者
或者![]() ,
,
故答案为:![]() 或者
或者![]() ;
;


科目:初中数学 来源: 题型:
【题目】在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.
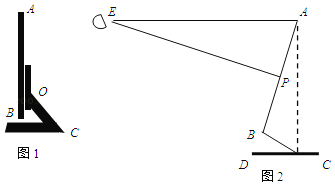
(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距![]() 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是
一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是![]() 以快车开始行驶计时,设时间为
以快车开始行驶计时,设时间为![]() , 两车之间的距离为
, 两车之间的距离为![]() ,图中的折线是
,图中的折线是![]() 与
与![]() 的函数关系的部分图象,根据图象解决以下问题:
的函数关系的部分图象,根据图象解决以下问题:

(1)慢车的速度是_ _![]() ,点
,点![]() 的坐标是_ _;
的坐标是_ _;
(2)线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式是_ ;
之间的函数关系式是_ ;
(3)试在图中补全点![]() 以后的图象.
以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知网格的小正方形的边长均为1,格点三角形ABC如图所示,请用没有刻度的直尺画出满足条件的图形
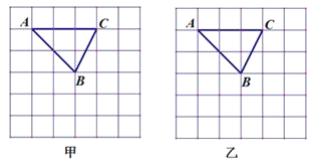
(1)在甲图中,画出△![]() ,且相似比为2:1,各顶点都在格点上.
,且相似比为2:1,各顶点都在格点上.
(2)在乙图中,把线段AB三等分.
查看答案和解析>>
科目:初中数学 来源: 题型:
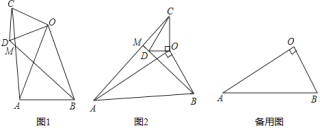
【题目】(1)问题发现:如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=36°,连接AC,BD交于点M.①![]() 的值为 ;②∠AMB的度数为 ;
的值为 ;②∠AMB的度数为 ;
(2)类比探究 :如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数.
的值及∠AMB的度数.
(3)拓展延伸:在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
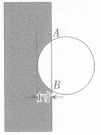
A.13B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
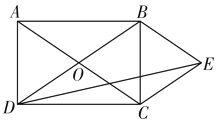
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,AB∶BC=3∶2,过点B作BE∥AC,过点C作CE∥DB,BE,CE交于点E,连接DE,则tan∠EDC等于()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
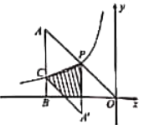
【题目】如图点P为双曲线![]() 上一动点.连接OP并延长到点A,使
上一动点.连接OP并延长到点A,使![]() ,过点A作x轴的垂线,垂足为B,交双曲线于点C.当
,过点A作x轴的垂线,垂足为B,交双曲线于点C.当![]() 时,连接PC,将
时,连接PC,将![]() 沿直线PC进行翻折,则翻折后的
沿直线PC进行翻折,则翻折后的![]() 与四边形BOPC的重叠部分(图中阴影部分)的面积是_______________
与四边形BOPC的重叠部分(图中阴影部分)的面积是_______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com