
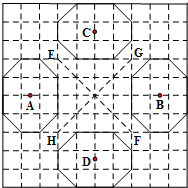
 15、在边长为1的正方形网络格中,由4个相同八边形组成“十字”形图案,小明为了发现其图案的变化过程,以八边形A为“基本图形”设计了以下三种变换方案(图中EF,GH分别为水平线AB和铅垂线CD的夹角的平分线),请你将他的方案补充完整:
15、在边长为1的正方形网络格中,由4个相同八边形组成“十字”形图案,小明为了发现其图案的变化过程,以八边形A为“基本图形”设计了以下三种变换方案(图中EF,GH分别为水平线AB和铅垂线CD的夹角的平分线),请你将他的方案补充完整: 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
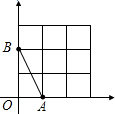 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在平面直角坐标系中,A、B、C、D均在边长为1的正方形网格格点上.
如图所示,在平面直角坐标系中,A、B、C、D均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
1.求线段AB所在直线的函数关系式,并写出当0≤y≤2时,自变量x的取值范围;
2.将线段AB绕点B逆时针旋转90°,得到线段BC,若直线BC的函数关系式为y=kx+b,则y随x的增大而 (填“增大”或“减小”).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图8,在平面直角坐标系中,![]() 、
、![]() 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.
(1)求线段![]() 所在直线的函数解析式,并写出当
所在直线的函数解析式,并写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
 (2)将线段
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,请在指定位置画出线段
,请在指定位置画出线段![]() .若直线
.若直线![]() 的函数解析式为
的函数解析式为![]() ,则
,则![]() 随
随![]() 的增大而 (填“增大”或“减小”).
的增大而 (填“增大”或“减小”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com