
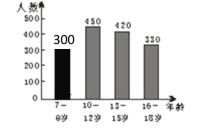
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
【答案】(1)1500;(2)详见解析;(3)108°;(5)50000.
【解析】
(1)根据16-18岁的近视人数和所占总调查人数的百分率即可求出总调查人数;
(2)计算出7-9岁的近视人数即可补全条形统计图;
(3)求出10-12岁的近视人数占总调查人数的百分率,再乘360°即可;
(4)求出7-12岁的近视学生人数占总调查人数的百分率,再乘该区总人数即可.
解:(1)这次抽样调查中共调查了近视学生人数为:330÷22%=1500人
故答案为:1500
(2)7-9岁的近视人数为:![]() 人
人
补全条形统计图如下:
(3)10-12岁部分的圆心角的度数是![]()
故答案为:![]()
(4)10万人=100000人
估计其中7-12岁的近视学生人数为![]() 人
人
答:7-12岁的近视学生人数约50000人.


科目:初中数学 来源: 题型:
【题目】如图,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.则这根芦苇的长度是( )

A. 10尺 B. 11尺 C. 12尺 D. 13尺
查看答案和解析>>
科目:初中数学 来源: 题型:
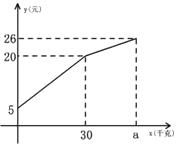
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018中国重庆开州汉丰湖国际摩托艇公开赛第二年举办.邻近区县一旅行社去年组团观看比赛,全团共花费9600元.今年赛事宣传工作得力,该旅行社继续组团前来观看比赛,人数比去年增加了![]() ,总费用增加了3900元,人均费用反而下降了20元.
,总费用增加了3900元,人均费用反而下降了20元.
(1)求该旅行社今年有多少人前来观看赛事?
(2)今年该旅行社本次费用中,其它费用不低于交通费的2倍,求人均交通费最多为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:数学兴趣一小组的同学对完全平方公式进行研究:因![]() ,将左边展开得到
,将左边展开得到![]() ,移项可得:
,移项可得:![]() .
.
数学兴趣二小组受兴趣一小组的启示,继续研究发现:对于任意两个非负数![]() 、
、![]() ,都存在
,都存在![]() ,并进一步发现,两个非负数
,并进一步发现,两个非负数![]() 、
、![]() 的和一定存在着一个最小值.
的和一定存在着一个最小值.
根据材料,解答下列问题:
(1)![]() __________(
__________(![]() ,
,![]() );
);![]() ___________(
___________(![]() );
);
(2)求![]() 的最小值;
的最小值;
(3)已知![]() ,当
,当![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
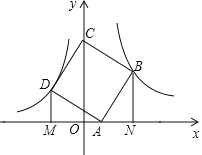
(1)k的值为___;
(2)求证:△ADM≌△BAN;
(3)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
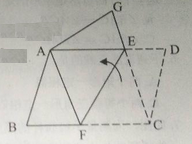
【题目】如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G出。
(1)如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?
(2)试判断四边形AFCE的形状,并说明你是怎样判断的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
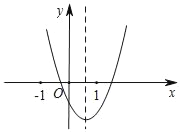
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com