
【题目】一元二次方程ax2+bx+c=0中,若a>0,b<0,c<0,则这个方程根的情况是( )
A.有两个正根
B.有两个负根
C.有一正根一负根且正根绝对值大
D.有一正根一负根且负根绝对值大
【答案】C
【解析】∵a>0,b<0,c<0,
∴△=b2﹣4ac>0, ![]() <0,﹣
<0,﹣ ![]() >0,
>0,
∴一元二次方程ax2+bx+c=0有两个不相等的实数根,且两根异号,正根的绝对值较大.
所以答案是:C.
【考点精析】根据题目的已知条件,利用求根公式和根与系数的关系的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
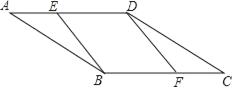
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组 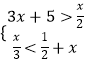 的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则 ![]() = .
= . 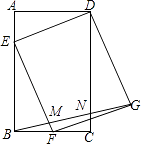
查看答案和解析>>
科目:初中数学 来源: 题型:
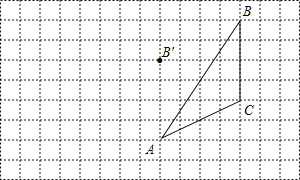
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1 是一个长为 4a、宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图 2).
(1)图 2 中的阴影部分的面积为 ;(用 a、b 的代数式表示)
(2)观察图 2 请你写出a b2 、a b2 、ab 之间的等量关系是 ;
(3)根据⑵中的结论,若 x y 5 , x y ![]() ,则 x y2 =_______.
,则 x y2 =_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com