

分析 (1)根据点A的坐标可以求得OA长,再由△AB0的面积为8可以求出m的值;
(2)根据三角形内角平分线的交点为三角形的内心以及三角形外角的性质,可以得出∠ACH=∠BCF;
(3)由三角形内角和定理和角平分线的性质可以推导出∠D-∠CBO的值.
解答 解:(1)∵A(0,4)
∴OA=4.
∵点B(m,n)在第一象限内,△AB0的面积为8,
∴$\frac{1}{2}$×4m=8
解得m=4;
(2)∵OF、AE为△ABO的角平分线,OF、AE相交于点C,
∴∠AOF=∠BOF=$\frac{1}{2}$∠AOB,∠OAE=∠BAE=$\frac{1}{2}$∠OAB,∠ABC=∠OBC=$\frac{1}{2}$∠ABO.
∵CH为△ACO的高,
∴∠ACH=90°.
∵∠BCF为△COB外角,
∴∠BCF=∠BOF+∠OBC=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠ABO=$\frac{1}{2}$(∠AOB+∠ABO)=$\frac{1}{2}$(180°-∠OAB)
∵∠ACH=90°-∠OAE=$\frac{1}{2}$(180°-∠OAB)
∴∠ACH=∠BCF;
(3)当B点运动时,∠D-∠CBO的值改变
证明:∵OD为OB与x轴正半轴夹角的平分线,
∴∠BOD=$\frac{1}{2}$(90°-∠AOB).
在△AOD中
∠D=180°-∠AOD-∠AOD=180°-$\frac{1}{2}$∠OAB-∠AOB-$\frac{1}{2}$∠BOD
=135°-$\frac{1}{2}$(∠OAB+∠AOB)
=135°-$\frac{1}{2}$(180°-∠AOB)
=45°+$\frac{1}{2}$∠ABO.
∴∠D-∠CBO=45°.
∴当B点运动时,∠D-∠CBO的值不改变.
点评 本题主要考查的是平面直角坐标系中点的坐标特征、角平分线的性质、三角形的内角和定理以及三角形的外角性质,掌握三角形的内角和定理以及三角形的外角性质是解决此题的关键.


科目:初中数学 来源: 题型:解答题
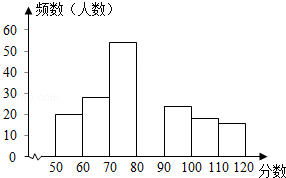 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:| 分数段 | 频数 | 频率 |
| 50≤x<60 | 20 | 0.10 |
| 60≤x<70 | 28 | b |
| 70≤x<80 | 54 | 0.27 |
| 80≤x<90 | a | 0.20 |
| 90≤x<100 | 24 | 0.12 |
| 100≤x<110 | 18 | 0.09 |
| 110≤x<120 | 16 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
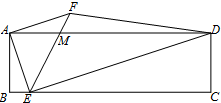 如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.
如图,矩形ABCD中,E为BC边上一点,且AE⊥DE.将线段AE绕A点逆时针旋转90°,得到线段AF.连接EF,交AD于点M,连接DF.若BE=1,EF=2$\sqrt{5}$,则点M到DF的距离为$\frac{3}{4}$$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com