
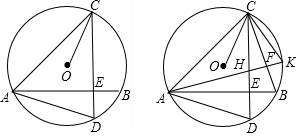
分析 (1)如图1,作直径CG,根据直径所对的圆周角是直角,再利用直角三角形两锐角互余,证明∠ACO=∠BAD;
(2)作辅助线,构建等边三角形,证明△OCK是等边三角形,所以得∠COK=60°,再根据同弧所对的圆心角是圆周角的二倍得∠CAK=30°,证明△AEH∽△AFB,根据比的值设EH=2x,BF=$\sqrt{7}$x,由△AFB∽△CFK和30°角的正切,求出CK=$\frac{2\sqrt{21}}{3}$并表示出FH和FK的长,在Rt△AFB中,根据勾股定理求出x的值,从而得出BF和FC的长,并计算BC的长即可.
解答 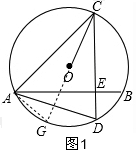 证明:(1)如图1,作直径CG,连接AG,
证明:(1)如图1,作直径CG,连接AG,
∴∠CAG=90°,
∴∠G+∠ACO=90°,
∵AB⊥CD,
∴∠AED=90°,
∴∠BAD+∠D=90°,
∵∠G=∠D,
∴∠ACO=∠BAD;
(2)如图2,∵射线CD沿CB翻折交⊙O于K,
∴∠DCB=∠BCK,
∴$\widehat{BD}=\widehat{BK}$,
∴∠BAD=∠BAK,
∵AB⊥CD,
∴∠BAD+∠D=90°,
∵∠B=∠D,
∴∠B+∠BAK=90°,
∴AK⊥BC,
设AK交BC于F,连接OK,
∴∠HFC=∠KFC=90°,
∵CF=CF,
∴△HCF≌△KCF,
∴CH=CK,
∵CH=OC,
∴CK=OC=OK,
∴△OCK是等边三角形,
∴∠COK=60°,
∴∠CAK=30°,
∵∠AEH=∠AFB=90°,∠BAK=∠BAK,
∴△AEH∽△AFB,
∴$\frac{AH}{AB}=\frac{EH}{BF}$=$\frac{4}{2\sqrt{7}}$=$\frac{2}{\sqrt{7}}$,
设EH=2x,BF=$\sqrt{7}$x,
∵∠BAF=∠BCK,∠AFB=∠CFK,
∴△AFB∽△CFK,
∴$\frac{CF}{AF}=\frac{CK}{AB}$,
∴tan∠CAK=tan30°=$\frac{CF}{AF}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{CK}{AB}=\frac{\sqrt{3}}{3}$,
∴$\frac{CK}{2\sqrt{7}}=\frac{\sqrt{3}}{3}$,
∴CK=$\frac{2\sqrt{21}}{3}$,
sin∠BAK=sin∠BCK=$\frac{EH}{AH}=\frac{FK}{CK}$,
∴$\frac{2x}{4}=\frac{FK}{\frac{2\sqrt{21}}{3}}$,
∴FK=$\frac{\sqrt{21}}{3}$x,
∴FH=FK=$\frac{\sqrt{21}}{3}$x,
在Rt△AFB中,AB2=AF2+BF2,
∴$(2\sqrt{7})^{2}=(4+\frac{\sqrt{21}}{3}x)^{2}+(\sqrt{7}x)^{2}$,
解得:x1=$\frac{2\sqrt{21}}{7}$,x2=-$\frac{3\sqrt{21}}{7}$(舍),
∴BF=$\sqrt{7}$x=$\sqrt{7}×\frac{2\sqrt{21}}{7}$=2$\sqrt{3}$,
FK=$\frac{\sqrt{21}}{3}$x=$\frac{\sqrt{21}}{3}$×$\frac{2\sqrt{21}}{7}$=2,
∴FC=$\sqrt{(\frac{2\sqrt{21}}{3})^{2}-{2}^{2}}$=$\frac{4\sqrt{3}}{3}$,
∴BC=BF+FC=2$\sqrt{3}$+$\frac{4\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$.
答:线段CB的长为$\frac{10\sqrt{3}}{3}$.
点评 此题考查了圆周角定理,勾股定理,全等三角形和相似三角形的判定与性质,以及折叠的性质,熟练掌握性质及定理是解本题的关键,尤其是第二问比较复杂,同角的三角函数与三角形相似相结合,通过设未知数,找等量关系列方程解出未知数的值,才使问题得以解决.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
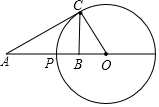 已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.
已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.
如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com