练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    阅读下面材料，再回答问题：

    有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”。

    解决下列问题：

    （1）菱形的“二分线”可以是                                    。

    （2）三角形的“二分线”可以是                                  。

    （3）在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.

     

    【答案】

    （1）菱形的一条对角线所在的直线。（或菱形的一组对边的中点所在的直线或菱形对角线交点的任意一条直线）。（2）三角形一边中线所在的直线。（3）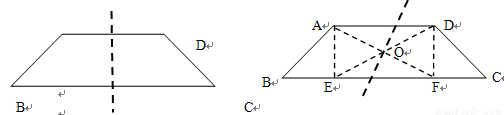

    【解析】解：（1）菱形的一条对角线所在的直线。（或菱形的一组对边的中点所在的直线或菱形对角线交点的任意一条直线）。

    （2）三角形一边中线所在的直线。

    （3）方法一：取上、下底的中点，过两点作直线得梯形的二分线（如图1）

    方法二：过A、D作AE⊥BC，DF⊥BC，垂足E、F，连接AF、DE相交于O，过点O任意作直线即为梯形的二分线（如图2）

    （1）利用菱形的轴对称性

           （2）三角形的中线把原三角形的面积分相等的两部分（等底同高） 

           （3）方法一：利用等腰梯形是轴对称图形，二分线就是它的对称轴

                方法二：二分线一定过等腰梯形的对称中心

    A
     
     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    阅读下面材料，再回答问题：
    一般地，如果函数y=f（x）对于自变量取值范围内的任意x，都有f（-x）=-f（x），那么y=f（x）就叫做奇函数；如果函数y=f（x）对于自变量取值范围内的任意x，都有f（-x）=f（x），那么y=f（x）就叫做偶函数．
    例如：f（x）=x3+x
    当x取任意实数时，f（-x）=（-x）3+（-x）=-x3-x=-（x3+x）
    即f（-x）=-f（x）
    所以f（x）=x3+x为奇函数
    又如f（x）=|x|
    当x取任意实数时，f（-x）=|-x|=|x|=f（x）
    即f（-x）=f（x）
    所以f（x）=|x|是偶函数
    问题（1）：下列函数中
    ①y=x4②y=x2+1③y=
    1
    x3

    ④y=
    		x+1
    ⑤y=x+
    1
    x

    所有奇函数是
     
    ，所有偶函数是
     
    （只填序号）
    问题（2）：请你再分别写出一个奇函数、一个偶函数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    24、阅读下面材料，再回答问题：
    有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”．
    解决下列问题：
    （1）菱形的“二分线”可以是
    菱形的一条对角线所在的直线
    ．
    （2）三角形的“二分线”可以是
    三角形一边中线所在的直线．
    ．
    （3）在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”，并说明你的画法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读下面材料，再回答问题．
    一般地，如果函数y=f（x）对于自变量取值范围内的任意x，都有f（-x）=f（x）．那么y=f（x）就叫偶函数．如果函数y=f（x）对于自变量取值范围内的任意x，都有f（-x）=-f（x）．那么y=f（x）就叫奇函数．
    例如：f（x）=x4
    当x取任意实数时，f（-x）=（-x）4=x4∴f（-x）=f（x）∴f（x）=x4是偶函数．
    又如：f（x）=2x3-x．
    当x取任意实数时，∵f（-x）=2（-x）3-（-x）=-2x3+x=-（2x3-x）∴f（-x）=-f（x）∴f（x）=2x3-x是奇函数．
    问题1：下列函数中：①y=x2+1②y=
    5
    x3
    ③y=
    		x+1
    ④y=x+
    1
    x
    ⑤y=x-2-2|x|
    是奇函数的有
     
    ；是偶函数的有
     
    （填序号）
    问题2：仿照例证明：函数④或⑤是奇函数还是偶函数（选择其中之一）     （4分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    先阅读下面材料，再回答问题．
    一般地，如果函数y的自变量x在a＜x＜b范围内，对于任意x1，x2，当a＜x1＜x2＜b时，总是有y1＜y2（yn是与xn对应的函数值），那么就说函数y在a＜x＜b范围内是增函数．
    例如：函数y=x2在正实数范围内是增函数．
    证明：在正实数范围内任取x1，x2，若x1＜x2，
    则y1-y2=x12-x22=（ x1-x2）（ x1+x2）
    因为x1＞0，x2＞0，x1＜x2
    所以x1+x2＞0，x1-x2＜0，（ x1-x2）（ x1+x2）＜0
    即y1-y2＜0，亦即y1＜y2，也就是当x1＜x2时，y1＜y2．
    所以函数y=x2在正实数范围内是增函数．
    问题：
    （1）下列函数中．①y=-2x（x为全体实数）；②y=-
    2
    x
    （x＞0）；③y=
    1
    x
    （x＞0）；在给定自变量x的取值范围内，是增函数的有
    ②
    ②
    ．
    （2）对于函数y=x2-2x+1，当自变量x
    ＞1
    ＞1
    时，函数值y随x的增大而增大．
    （3）说明函数y=-x2+4x，当x＜2时是增函数．

    查看答案和解析>>

    科目：初中数学 来源：2012届湖北省宜昌市长阳县九年级上学期期末检测数学试卷（带解析） 题型：解答题

    阅读下面材料，再回答问题：
    有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”，正方形的对角线所在的直线是正方形的“二分线”。
    解决下列问题：
    （1）菱形的“二分线”可以是                                   。
    （2）三角形的“二分线”可以是                                 。
    （3）在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.

    查看答案和解析>>

    同步练习册答案