
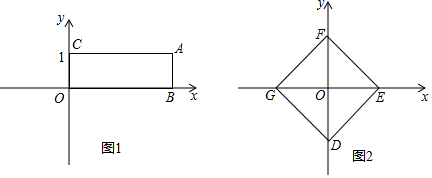
分析 (1)根据“垂点”的意义直接判断即可得出结论;
(2)根据“垂点”的意义建立方程即可得出结论;
(3)根据“垂点”的意义和矩形的面积建立方程即可得出结论;
(4)先确定出直线EF的解析式,利用“垂点”的意义建立方程,利用非负性即可确定出m的范围,即可得出结论.
解答 解:(1)∵P(1,2),
∴1+2=3,1×2=2,
∵2≠3,
∴点P不是“垂点”,
∵Q(2,-2),
∴2+2=4,2×2=4,
∴Q是“垂点”.
∵N($\frac{1}{2}$,-1),
∴$\frac{1}{2}$+1=$\frac{3}{2}$,$\frac{1}{2}$×1=$\frac{1}{2}$,
∵$\frac{3}{2}≠\frac{1}{2}$,
∴点N不是“垂点”,
故答案为:Q;
(2)∵点 M(-4,m)是第三象限的“垂点”,
∴4+(-m)=4×(-m),
∴m=-$\frac{4}{3}$,
故答案为:-$\frac{4}{3}$;
(3)设“垂点”的坐标为(a,b),
∴-a+b=-ab,
∵“垂点矩形”的面积为$\frac{16}{3}$,
∴-ab=$\frac{16}{3}$.
即:-a+b=-ab=$\frac{16}{3}$,
解得,a=-4,b=$\frac{4}{3}$或a=-$\frac{4}{3}$,b=4,
∴“垂点”的坐标为(-4,$\frac{4}{3}$)或(-$\frac{4}{3}$,4),
故答案为:(-4,$\frac{4}{3}$)或(-$\frac{4}{3}$,4),
(4)解:设点E(m,0)(m>0),
∵四边形EFGH是正方形,
∴F(0,m),y=-x+m.设边EF上的“垂点”的坐标为(a,-a+m),
∴a+(-a+m)=a(-a+m)
∴a2-am=-m,
∴(a-$\frac{m}{2}$)2=$\frac{{m}^{2}-4m}{4}$≥0,
∴m2-4m=m(m-4)≥0,
∵m>0,
∴m-4≥0,
∴m≥4,
∴m的最小值为4,
∴EG的最小值为2m=8,
故答案为8.
点评 此题是四边形的综合题,主要考查了正方形的性质,矩形的面积公式,理解新定义和应用新定义的能力,解本题的关键是用方程的思想解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 10千米 | B. | 12千米 | C. | 14千米 | D. | 16千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月利润(万元) | 1 | 2 | 3 | 4 |
| 人数 | 2 | 4 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com