
����Ŀ���������磬С�쵽���깬�μ�9������ʼ���赸���ݣ�С��8�����ӼҲ��г������ƻ���ǰ20min���С�첽����900m����һ���������ڼ������ϣ���������ԭ���ٶȵ�1.5����ԭ·���أ�8��25�ֵ�����У�
(1)��С��ԭ���IJ����ٶȣ�
(2)С��Ϊȷ��������8��40�ֵ������깬�����õ����ߺ���12km/h���ٶ����������г�������ԭ��·�������깬����С���ڼ����ֻ�ܵ������ʱ�䣿
���𰸡���1��С��ԭ�����ٶ�Ϊ60m/min��(2) С���ڼ����ֻ�ܵ���3min.
��������
��1����С��ԭ���IJ����ٶ�Ϊxm/min�������ٺ���ٶ�Ϊ1.5xm/min������ʱ��=·�̡��ٶȽ����������25min�����ɵó�����x�ķ�ʽ���̣���֮������ɵó����ۣ�
��2������·��=�ٶȡ�ʱ�����С��ҵ����깬�ľ��룬��ʱ��=·�̡��ٶȿ����С���ﳵ�ϵ����깬����ʱ�䣬�ٽ�ϲ�����8��40�ֵ�������٣��������С���ڼ���ൢ���ʱ�䣮
��1����С��ԭ���IJ����ٶ�Ϊxm/min�������ٺ���ٶ�Ϊ1.5xm/min����������ã�![]() 25
25
��ã�x=60��
�����飬x=60��ԭ���̵ĸ���
��С��ԭ���IJ����ٶ�Ϊ60m/min��
��2��С��ҵ����깬�ľ���Ϊ60��40=2400��m����С���ﳵ�������깬����ʱ��Ϊ2400��12000=0.2h=12��min����С���ڼ�����ܵ����ʱ��Ϊ40��25��12=3��min����
��С���ڼ����ֻ�ܵ���3min��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ҩƷ�г�������ҩƷ�۸��ǹ��ҵĻ�������֮һ�����ݹ��ҡ�ҩƷ�������۰취����ijʡ�йز��Ź涨���г���ͨҩƷ�����ۼ۸ó������۵�15%�����������Ϣ����������⣺
��1������ǰ����������ҩƷÿ�еij����۸�֮��Ϊ6.6Ԫ�����������м价�ڣ�����ҩƷÿ�е����ۼ۸�ȳ����۸��5����2.2Ԫ������ҩƷÿ�е����ۼ۸��dz����۸��6��������ҩƷÿ�е����ۼ۸�֮��Ϊ33.8Ԫ����ô����ǰ�ס�������ҩƷÿ�е����ۼ۸�ֱ��Ƕ���Ԫ��
��2�����ۺ�ijҩƷ�����̽������ļס�������ҩƷ�ֱ���ÿ��8Ԫ��5Ԫ�ļ۸����۸�ҽԺ��ҽԺ����ʵ������������Լ���ҩƷÿ�мӼ�15%��������ҩƷÿ�мӼ�10%�����۸����ߣ�ʵ�ʽ�ҩʱ��������ҩƷ����ÿ10��Ϊ1����а�װ�����ڸ�ҽԺ���Ӿ����̴�������������ҩƷ��100�䣬��������ҩƷ������40�䣬��������ҩƷ����������900Ԫ�����ʹ���ʱ���ļ��ִ��䷽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�ڲμӡ��������ǣ�����Ȫ�ǡ��黭�����У�����ʦ��ȫУ30�����������ȡ��4���ࣨ��A��B��C��D��ʾ�����������������������������˷���ͳ�ƣ�������������������ͳ��ͼ��
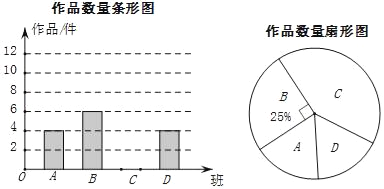
�����������Ϣ���ش��������⣺
��l������ʦ���õĵ��鷽ʽ���� ������ղ顱�������顱����
��2���벹����������ͳ��ͼ������������ͳ��ͼ��C����Ʒ��������Ӧ��Բ�ĽǶ����� ����
��3�������ȫУ��������Ʒ��ʲ����
��4�����ȫ֦��������Ʒ����5�����һ�Ƚ���������3��������������2��������Ů������Ҫ�ڻ��һ���Ƚ���������ѡȡ���˲μӱ�����̸�ᣬ�������б�����״ͼ�ķ�������ǡ��ѡȡ������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() x����A1����Ϊ(1��0)������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3��������������������ȥ����A4������Ϊ______����An______��
x����A1����Ϊ(1��0)������A1��x��Ĵ��߽�ֱ���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2���ٹ���A2��x��Ĵ��߽�ֱ���ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3��������������������ȥ����A4������Ϊ______����An______��
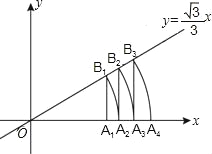
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD����O���ڽ������Σ�E����BD���е㣬��C����O��һ������DBC=��A������OE�ӳ���Բ�ཻ�ڵ�F����BC�ཻ�ڵ�C��
��1����֤��BC����O�����ߣ�
��2������O�İ뾶Ϊ6��BC=8������BD�ij���
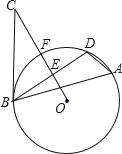
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABCD�У��߶�EF�ֱ�AD��AC��BC�ڵ�E��O��F��EF��AC��AO=CO��
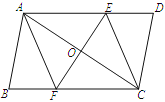
��1����֤����AOE�ա�COF��
��2���ڱ������֪�����У���һ���������ȥ��������Ӱ�죨1����֤��������Ϊ�������������� ��ֱ��д�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��b��c�dz�������c��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1,0)��
��b��c�dz�������c��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1,0)��
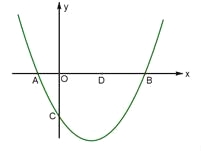
��1��b��______����B�ĺ�����Ϊ_______������������ú�c�Ĵ���ʽ��ʾ����
��2������BC������A��ֱ��AE//BC���������߽��ڵ�E����D��x����һ�㣬����Ϊ(2,0)����C��D��E������ͬһֱ����ʱ���������ߵĽ���ʽ��
��3���ڣ�2���������£���P��x���·����������ϵ�һ���㣬����PB��PC������PBC�����ΪS������S��ȡֵ��Χ��������PBC�����SΪ������������������PBC����_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=��x+4����ֱ��l��ȡ��B1����B1�ֱ���x�ᣬy�������ߣ���x����A1����y����C1��ʹ�ı���OA1B1C1Ϊ�����Σ���ֱ��l��ȡ��B2����B2�ֱ���x�ᣬA1B1�����ߣ���x����A2����A1B1��C2��ʹ�ı���A1A2B2C2Ϊ�����Σ����˷�����ֱ��l��˳��ȡ��B3��B4������Bn��������������A2A3B3C3��A3A4B4C4������An��1AnBnCn����A3������Ϊ___��B5������Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
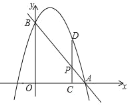
����Ŀ����ͼ����ֱ֪��y����x+4�ֱ�x�ᡢy���ڵ�A��B�������߹�y��ax2+bx+c����A��B���㣬��P���߶�AB��һ���㣬����P��PC��x���ڵ�C�����������ڵ�D��
��1���������ߵĽ���ʽΪy����![]() x2+x+4�����䶥��ΪM����Գ��ύAB�ڵ�N��
x2+x+4�����䶥��ΪM����Գ��ύAB�ڵ�N��
�����M��N�����ꣻ
���Ƿ���ڵ�P��ʹ�ı���MNPDΪ���Σ���˵�����ɣ�
��2������P�ĺ�����Ϊ2ʱ���Ƿ���������������ߣ�ʹ����B��P��DΪ�������������ֱ�������Σ������ڣ�������������������ߵĽ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com