
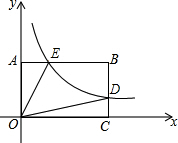
 如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③.
如图,反比例函数y=$\frac{k}{x}$(k>0)图象过矩形OABC边BC中点D交AB于点E,四边形ODBE的面积为2,则结论:①S△OAE=S△OCD;②E为AB中点;③k=2;④AO=AE,其中正确的序号为①②③. 分析 设点D的坐标为(a,b),点E的坐标为(c,d),用k表示出S△OAE和S△OCD判断①;
根据S△OAE=$\frac{1}{2}$S△OBA,得出AE=BE,判断②;
根据反比例函数的系数的几何意义判断③;
根据①的结论,得到点E的坐标,判断④.
解答 解: 连接OB,
连接OB,
设点D的坐标为(a,b),点E的坐标为(c,d),
∵点D、点E在反比例函数y=$\frac{k}{x}$图象上,
∴ab=k,cd=k,
S△OAE=$\frac{1}{2}$cd=$\frac{1}{2}$k,S△OCD=$\frac{1}{2}$ab=$\frac{1}{2}k$,
∴S△OAE=S△OCD,①正确;
∵点D是BC中点,
∴S△OCD=$\frac{1}{2}$S△OBC,
∴S△OAE=$\frac{1}{2}$S△OBA,
∴AE=BE,即E为AB中点,②正确;
∵四边形ODBE的面积为2,
∴S△OCD=1,
∴$\frac{1}{2}k$=1,则k=2,③正确;
∵点E的坐标为($\frac{1}{2}$AB,OA),
∴AO=AE不一定成立,④错误,
故答案为:①②③.
点评 本题考查的是反比例函数的系数的几何意义和反比例函数的性质,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:填空题
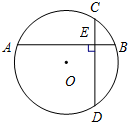 如图,两条互相垂直的弦将⊙O分成四部分,相对的两部分面积之和分别记为S1、S2,若圆心O到两弦的距离分别为4和6,则|S1-S2|=96.
如图,两条互相垂直的弦将⊙O分成四部分,相对的两部分面积之和分别记为S1、S2,若圆心O到两弦的距离分别为4和6,则|S1-S2|=96.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com