
分析 先把等式左边化简得到$\frac{21\sqrt{2}}{4}$=a+b$\sqrt{2}$,由a,b为有理数,则得到a=0,b=$\frac{21}{4}$,即可计算ab=0.
解答 解:∵$\sqrt{8}$+$\sqrt{18}$+$\sqrt{\frac{1}{8}}$=2$\sqrt{2}$+3$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=$\frac{21\sqrt{2}}{4}$,
∴$\frac{21\sqrt{2}}{4}$=a+b$\sqrt{2}$,
∴a=0,b=$\frac{21}{4}$,
∴ab=0,
故答案为0.
点评 本题考查了二次根式的加减法:先把二次根式化为最简二次根式,然后合并同类二次根式.


科目:初中数学 来源: 题型:选择题
| A. | 不盈不亏 | B. | 盈利50元 | C. | 盈利8元 | D. | 亏损8元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 赔了100元 | B. | 赚了100元 | C. | 不赔不赚 | D. | 赚了180元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
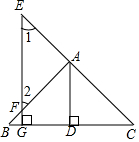 如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.
如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC,FG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①对,②错 | B. | ①错,②对 | C. | ①②都错 | D. | ①②都对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com