
分析 根据题意得出a=-$\frac{1}{2}$,b=2,再化简原式,代入求值即可.
解答 解:∵|a+$\frac{1}{2}$|与b2-4b+4互为相反数,
∴|a+$\frac{1}{2}$|+b2-4b+4=0,
∴a=-$\frac{1}{2}$,b=2,
∴原式=$\frac{a-b}{a+b}$•$\frac{(a+b)(a-b)}{{a}^{2}+{b}^{2}}$-$\frac{a+b}{ab}$•$\frac{ab(a+b)}{{a}^{2}+{b}^{2}}$,
=$\frac{(a-b)^{2}}{{a}^{2}{+b}^{2}}$-$\frac{(a+b)^{2}}{{a}^{2}+{b}^{2}}$
=$\frac{(a-b+a+b)(a-b-a-b)}{{a}^{2}+{b}^{2}}$
=$\frac{-4ab}{{a}^{2}+{b}^{2}}$.
当a=-$\frac{1}{2}$,b=2时,原式=$\frac{-4×(-\frac{1}{2})×2}{(-\frac{1}{2})^{2}+{2}^{2}}$=$\frac{4}{4\frac{1}{4}}$=$\frac{16}{17}$.
点评 本题考查了分式的化简求值,掌握相反数的性质以及分式的约分、因式分解是解题的关键.


科目:初中数学 来源: 题型:选择题
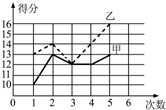 甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )
甲、乙两人参加某体育项目训练,为了便于了解他们的训练情况,教练将他们最近五次的训练成绩用如图所示的复式统计图表示出来,则下面结论错误的是( )| A. | 甲的第三次成绩与第四次成绩相同 | |
| B. | 第三次训练,甲、乙两人的成绩相同 | |
| C. | 第四次训练,甲的成绩比乙的成绩少2分 | |
| D. | 五次训练,甲的成绩都比乙的成绩高 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
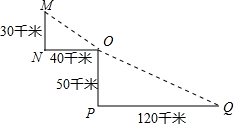 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a-1}=\frac{2}{a-2}$ | B. | $\frac{1}{a-1}=\frac{a+1}{{{a^2}-1}}$(a≠-1) | ||
| C. | $\frac{1}{a-1}=\frac{a-1}{{{a^2}-1}}$ | D. | $\frac{1}{a-1}=\frac{-1}{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
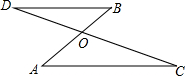 如图.BD∥AC,AB与CD相交于点O,已知△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=2,求AB的长.
如图.BD∥AC,AB与CD相交于点O,已知△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=2,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com