
分析 (1)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)先方程两边都乘以x-2得出1=x-1-3(x-2),求出方程的解,再进行检验即可.
解答 解:(1)x2-2x-1=0,
x2-2x+1=2,
(x-1)2=2,
$x-1=±\sqrt{2}$
∴${x_1}=1+\sqrt{2}$,${x_2}=1-\sqrt{2}$;
(2)$\frac{1}{x-2}=\frac{1-x}{2-x}-3$,
方程两边斗乘以x-2得:1=x-1-3(x-2),
解得:x=2,
检验:当x=2时,x-2=0,
所以x=2不是原方程的解,
即原方程无解.
点评 本题考查了解一元二次方程和解分式方程的应用,解(1)小题的关键是配方,解(2)小题的关键是能把分式方程转化成整式方程,难度适中.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
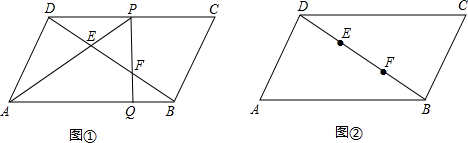
| AQ长度 | BQ长度 | AQ、BQ间的关系 | |
| 图①中 | 2.7 | 0.9 | AQ=3BQ |
| 图②中 | 3.3 | 1.1 | AQ=3BQ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
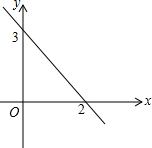 如图,一次函数y=kx+b(k≠0)的图象如图所示,在第一象限内的图象上是否存在一定P,使过点P所作的两坐标轴的垂线与两坐标轴围成的四边形的面积为2?若存在,求出点P的坐标;若不存在,请说明理由.
如图,一次函数y=kx+b(k≠0)的图象如图所示,在第一象限内的图象上是否存在一定P,使过点P所作的两坐标轴的垂线与两坐标轴围成的四边形的面积为2?若存在,求出点P的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com