
【题目】如图,已知![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 为原点,点
为原点,点![]() 表示的数为6,
表示的数为6,![]() ,
,![]() .
.
![]()
(1)写出数轴上点![]() 、
、![]() 表示的数;
表示的数;
(2)动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,沿数轴向右匀速运动.点
同时出发,沿数轴向右匀速运动.点![]() 的速度是每秒6个单位长度,点
的速度是每秒6个单位长度,点![]() 的速度是每秒3个单位长度,点
的速度是每秒3个单位长度,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
①求数轴上点![]() 、
、![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②当![]() 、
、![]() 、
、![]() 三个点中的其中一个点是另两点构成的线段的中点的时候,求
三个点中的其中一个点是另两点构成的线段的中点的时候,求![]() 的值.
的值.
【答案】(1)点![]() 表示-10,点
表示-10,点![]() 表示2;(2)①点
表示2;(2)①点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ;②t为2秒或
;②t为2秒或![]() 秒或20秒.
秒或20秒.
【解析】
(1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN![]() CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②分三种情况讨论即可.
(1)∵C表示的数为6,BC=4,
∴OB=6﹣4=2,
∴B点表示2.
∵AB=12,
∴AO=12﹣2=10,
∴A点表示﹣10;
(2)①由题意得:AP=6t,CQ=3t,如图所示.
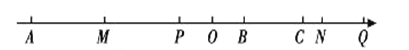
由M为AP中点,得AM=![]() AP=3t,
AP=3t,
点M表示的数是-10+3t,
点N在CQ上,CN=![]() CQ,
CQ,
∴CN=t,
点N表示的数是6+t.
②分三种情况讨论:
i)若点B为MN中点.
∵点M表示的数是-10+3t,点N表示的数是6+t,B点表示2,
∴(-10+3t)+(6+t)=2×2,
解得:t=2;
![]()
ii)若点M为BN中点.
∵点M表示的数是-10+3t,点N表示的数是6+t,B点表示2,
∴2+(6+t)=2(-10+3t),
解得:t=![]() ;
;
![]()
iii)若点N为BM中点.
∵点M表示的数是-10+3t,点N表示的数是6+t,B点表示2,
∴(-10+3t)+2=2(6+t),
解得:t=20.
![]()
综上所述:当t为2秒或![]() 秒或20秒时,M、B、N三个点中的其中一个点是其他两点构成的线段的中点.
秒或20秒时,M、B、N三个点中的其中一个点是其他两点构成的线段的中点.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]()
![]() 的图象只有一个交点
的图象只有一个交点![]() .
.
(1)求反比例函数的解析式;
(2)在函数![]() 的图象上取异于点
的图象上取异于点![]() 的一点
的一点![]() ,作
,作![]() 轴于点
轴于点![]() ,连接
,连接![]() 交直线于点
交直线于点![]() .设直线与
.设直线与![]() 轴交于点
轴交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求点
倍,求点![]() 的坐标.
的坐标.
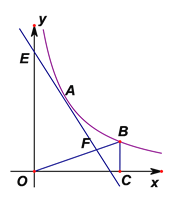
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“足球在身边”的专题调查活动,采取随机抽样的方法进行问卷调查,调查结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,并将调查结果绘制成两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题:
(1)被调查的学生共有___人.在扇形统计图中,表示“比较了解”的扇形的圆心角度数为___度
(2)请用列表法或树状分析从![]() 名男生和
名男生和![]() 名女生中随机抽取
名女生中随机抽取![]() 名学生参加“足球在身边”的知识竞赛,抽中
名学生参加“足球在身边”的知识竞赛,抽中![]() 男
男![]() 女的概率.
女的概率.
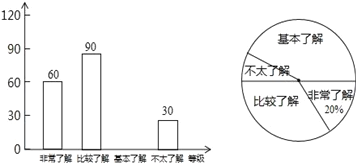
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图1所示的拼接图形(实线部分),经折叠后发现还少一个面,请在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示.只要画出一种即可)
(2)如图2所示的几何体是由几个相同的正方体搭成的,请画出它从正面看的形状图.
(3)如图3是几个正方体所组成的几何体从上面看的形状图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体从左面看的形状图.
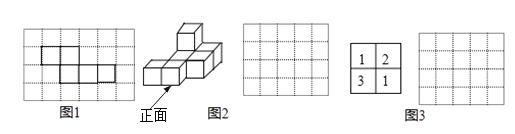
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成,过去,某市网民通过电脑拨号上“因特网”的费用为电话费每3分钟0.18元,上网费每小时7.2元,现在,该市对上“因特网”的费用作了调整:电话费每3分钟0.22元,上网费为每月不超过60小时,按每小时4元计算;超过60小时部分,按每小时8元计算.
(1)根据调整后的规定,用解析式表示网民每月上“因特网”的费用![]() (元)与上网时间
(元)与上网时间![]() 之间的函数关系式;
之间的函数关系式;
(2)资费调整前,网民小刚在其家庭经济预算中,一直有一笔每月70小时的上网费用支出,因“因特网”资费调整后,小刚要想不超过其家庭经济预算中的上网费用支出,他现在每月至多可上网多少小时?
(3)从资费调整前后该市网民上网费用的支出增减情况分析,哪些网民支出增加?哪些网民支出减少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述:
①最小的正整数是![]() ;
;
②若![]() 是一个负数,则
是一个负数,则![]() 一定是负数;
一定是负数;
③用一个平面去截正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
其中正确的个数有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊毕达哥拉斯学派的数学家经常用小石子摆成各种形状来研究数学问题.
如图1,由于这些三角形是由1个,3个,6个,10个,… 小石子摆成的,所以他们称1,3,6,10,…,这些数为三边形数;类似的,如图2,他们称1,4,9,16,…,这样的数为四边形数.

(1)既是三边形数,又是四边形数,且大于1的最小正整数是 ;
(2)如果记第n个k边形小石子的个数为![]() (k≥3),那么易得
(k≥3),那么易得![]() ,
,![]() ,
,![]() .
.
① ![]() ;
;![]() ;
;
② ![]() ;
;![]() ;
;
③ 如果![]() ,那么
,那么![]() ;
;
(3)如果进一步研究发现![]() ,
,![]() ,…,那么
,…,那么![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com