
分析 ①原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
②原式逆用乘法分配律计算即可得到结果;
③原式利用乘方的意义,以及乘法分配律计算即可得到结果;
④方程去括号,移项合并,把x系数化为1,即可求出解;
⑤方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
⑥方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:①原式=-1-54-54=-109;
②原式=$\frac{2}{3}$×(-18+13-4)=$\frac{2}{3}$×(-9)=-6;
③原式=-16-6+4+2=-16;
④去括号得:4x+2=3-2x+4,
移项合并得:6x=5,
解得:x=$\frac{5}{6}$;
⑤去分母得:8-4y+5=6-2y,
移项合并得:-2y=-7,
解得:y=$\frac{7}{2}$;
⑥方程整理得:$\frac{3x+5}{2}$-$\frac{2x-1}{3}$=1,
去分母得:9x+15-4x+2=6,
移项合并得:5x=-11,
解得:x=-2.2.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
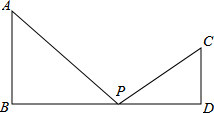 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,-6) | B. | (-4,6) | C. | (6,-4) | D. | (-6,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}{x^2}+2x+1=0$ | B. | 0.1x2-0.5x+1.8=0 | ||
| C. | $\frac{1}{2}{x^2}=1-\frac{3}{5}x$ | D. | x2+x-1=(x+1)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com