
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y= 于点D,过D作两坐标轴的垂线DC、DE,连接OD.
于点D,过D作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证AD·BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.
(1)由y=x+b得A(b,0),B(0,-b),即可得到∠DAC=∠OAB="45" º,再结合DC⊥x轴,DE⊥y轴可证得∠ACD=∠CDE=90º,从而可以证得结论;(2)由(1)知△ACD和△BDE均为等腰直角三角形,即可证得AD=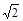 CD,BD=
CD,BD=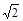 DE,则可得AD·BD=2CD·DE=2×2=4为定值;(3)y=x-1
DE,则可得AD·BD=2CD·DE=2×2=4为定值;(3)y=x-1
解析试题分析:(1)由y=x+b得A(b,0),B(0,-b),即可得到∠DAC=∠OAB="45" º,再结合DC⊥x轴,DE⊥y轴可证得∠ACD=∠CDE=90º,从而可以证得结论;
(2)由(1)知△ACD和△BDE均为等腰直角三角形,即可证得AD=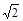 CD,BD=
CD,BD=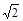 DE,则可得AD·BD=2CD·DE=2×2=4为定值;
DE,则可得AD·BD=2CD·DE=2×2=4为定值;
(3)若OBCD为平行四边形,则AO=AC,OB=CD,由(1)知AO=BO,AC=CD,设OB="a" (a>0),则可得B(0,-a),D(2a,a),由D在y= 上即可求得a的值,从而可以求得结果.
上即可求得a的值,从而可以求得结果.
解:(1)由y=x+b得A(b,0),B(0,-b).
∴∠DAC=∠OAB="45" º
∵DC⊥x轴,DE⊥y轴
∴∠ACD=∠CDE=90º
∴∠ADC=45º ,即AD平分∠CDE;
(2)由(1)知△ACD和△BDE均为等腰直角三角形.
∴AD=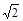 CD,BD=
CD,BD=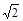 DE
DE
∴AD·BD=2CD·DE=2×2=4为定值;
(3)存在直线AB,使得OBCD为平行四边形.
若OBCD为平行四边形,则AO=AC,OB=CD.
由(1)知AO=BO,AC=CD
设OB="a" (a>0),
∴B(0,-a),D(2a,a)
∵D在y= 上,
上,
∴2a·a=2,解得a=±1(负数舍去)
∴B(0,-1),D(2,1).
又B在y=x+b上,
∴b=-1
即存在直线AB:y=x-1,使得四边形OBCD为平行四边形.
考点:函数问题的综合题
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
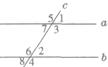 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
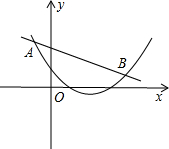
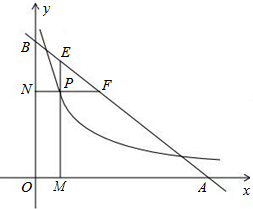 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=| 4 |
| x |
| A、8 | ||
| B、6 | ||
| C、4 | ||
D、6
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com