
【题目】根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
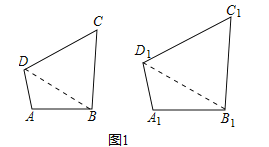
(2)如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,![]() ,求证:四边形ABCD与四边形A1B1C1D1相似.
,求证:四边形ABCD与四边形A1B1C1D1相似.

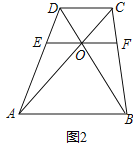
(3)如图2,四边形ABCD中,AB∥CD,AC与BD相交于点O,过点O作EF∥AB分别交AD,BC于点E,F.记四边形ABFE的面积为S1,四边形EFDE的面积为S2,若四边形ABFE与四边形EFCD相似,求![]() 的值.
的值.
【答案】(1)①假,②假,③真;(2)见解析 ;(3)![]()
【解析】
(1)根据相似多边形的定义即可判断.
(2)根据相似多边形的定义证明四边成比例,四个角相等即可.
(3)四边形ABFE与四边形EFCD相似,证明相似比是1即可解决问题,即证明DE=AE即可.
解(1)①四条边成比例的两个凸四边形相似,是假命题,角不一定相等.
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.
③两个大小不同的正方形相似.是真命题.
故答案为假,假,真.
(2)证明:分别连接BD,B1D1
![]() ,且
,且![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 四边形ABCD与四边形A1B1C1D1相似.
四边形ABCD与四边形A1B1C1D1相似.
(3)如图2中,
∵四边形ABFG与四边形EFCD相似
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即AE=DE
,即AE=DE
![]() ,
,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
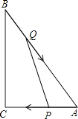
【题目】.如图,在RT△ABC中,∠C=90°,BC=8,AC=6,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动.当一点停止运动,另一点也随之停止运动.设点Q,P移动的时间为t秒.当t=____________ 秒时△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程mx2+(3﹣m)x﹣3=0(m为实数,m≠0).
(1) 试说明:此方程总有两个实数根.
(2) 如果此方程的两个实数根都为正整数,求整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC⊥BD垂足为点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接NF.
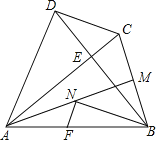
(1)判断线段MN与线段BM的位置关系与数量关系,说明理由;
(2)如果CD=5,求NF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E,连接OE
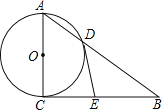
(1)求证:△DBE是等腰三角形
(2)求证:△COE∽△CAB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图
任务一:下面是小希设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
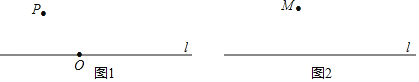
已知:直线l及直线外一点P.
求作:直线PQ,使得PQ∥l.
作法:如图
①在直线l上取一点O,连接OP,以点O为圆心,OP为半径画圆,交直线l与点A和点B;②连接AP,以点B为圆心,AP长为半径在直线l上方画弧交⊙O于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小希设计的尺规作图步骤完成下列问题:
(1)在图1中使用直尺和圆规,补全图形;(保留作图痕迹)
(2)证明:PQ∥l
任务二:已知:直线l及直线l外一点M.
请根据下列提供的数学原理,选择其一,在图2中使用直尺和圆规作直线MN,使得MN∥l.(保留作图痕迹,不写作法)
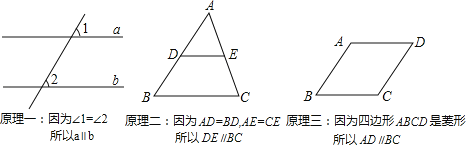
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 今年的销售价格 | 2 |
那么新款B型节能电动车至少要购进多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com