
 如图,在四边形ABCD中,点P是边BC上一动点,过点P作直线EF∥AB,且与∠ABC、∠CBG的角平分线分别相交于点E、F.
如图,在四边形ABCD中,点P是边BC上一动点,过点P作直线EF∥AB,且与∠ABC、∠CBG的角平分线分别相交于点E、F.分析 (1)首先利用平行线的性质以及角平分线的性质得出∠PEB=∠ABE,∠PBE=∠ABE,进而得出EP=BP,FP=BP,即可得出答案;
(2)根据“对角线互相平分的四边形是平行四边形”的判断定理,先证四边形BFCE是平行四边形,再证∠EBF=90°即可;
(3)如果矩形BFCE是正方形,那么EB=FB,那么∠BEF=∠BFE=45°,进而得出∠PEB=∠ABE=∠PBE=45°,求出∠ABC=90°.
解答 (1)证明:∵EF∥AB,∠ABE=∠EBP,∠GBF=∠FBP,
∴∠PEB=∠ABE,∠PBE=∠ABE,
∴∠PEB=∠PBE,
即EP=BP;
同理可证FP=BP,
所以EP=FP;
(2)当点P运动到BC边的中点时,四边形BFCE是矩形,
理由:∵PC=BP,由(1)得:EP=FP,
∴四边形CEBF是平行四边形,
∵∠ABE=∠EBP,∠GBF=∠FBP,
∴∠EBP+∠FBP=∠ABE+∠GBF=90°,
∴∠EBF=90°,
∴四边形BFCE是矩形;
(3)在(2)的基础上证明,
如果矩形BFCE是正方形,
那么EB=FB,
那么∠BEF=∠BFE=45°,
∴∠PEB=∠ABE=∠PBE=45°,
∴∠ABE+∠PBE=90°,即∠ABC=90°.
点评 此题主要考查了矩形的判定、正方形的判定以及角平分线的性质和平行线的性质等知识,正确掌握正方形的判定与性质是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=0 | B. | x≠1 | C. | x≥-5 | D. | x≥-5且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
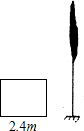 国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了学生的终身发展,某中学积极开展第二课堂,下面是该中学一部分学生参加五个学习小组的统计表和扇形统计图,请根据图表提供的信息回答下列问题:
为了学生的终身发展,某中学积极开展第二课堂,下面是该中学一部分学生参加五个学习小组的统计表和扇形统计图,请根据图表提供的信息回答下列问题:| 学习小组 | 体育 | 美术 | 音乐 | 写作 | 奥数 |
| 人数 | 75 | 75 | 54 | 30 | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com