
【题目】如图所示,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
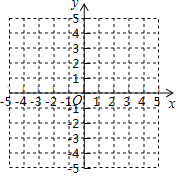
(1)在图中画出![]() ,
,![]() 的面积是_____________;
的面积是_____________;
(2)若点![]() 与点
与点![]() 关于
关于![]() 轴对称,则点
轴对称,则点![]() 的坐标为_____________;
的坐标为_____________;
(3)已知![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
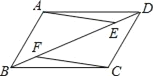
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,﹣2);
③抛物线的对称轴是:x=1;
④在对称轴左侧,y随x增大而增大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
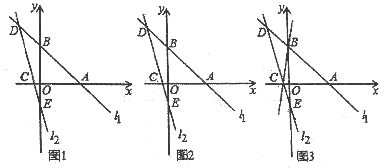
【题目】如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒![]() 个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
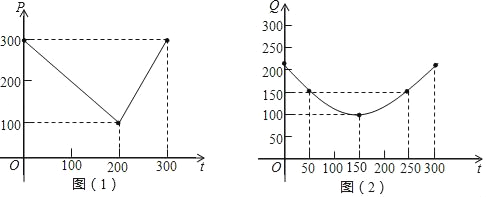
【题目】(7分)某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段Q=![]() (t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)
(1)写出图(1)表示的市场售价P与时间t的函数关系式;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).

A.2.5B.2C.1.5D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com