

分析 (1)根据△AOB的面积列出方程即可解决问题;
(2)当0<t<2时①∠ANM=∠OMN+∠BAN.如图2中,过N点作NH∥AB,利用平行的性质证明即可.②根据S四边形AMON=S四绞刑ABOM-S△ABN,计算即可;
(3)分两种情形列出方程即可解决问题;
解答 解:(1)如图1中,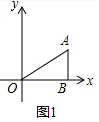
∵S△AOB=12,A(3a,2a),
∴$\frac{1}{2}$×3a×2a=12,
∴a2=4,
又∵a>0,
∴a=2.
(2)当0<t<2时
①∠ANM=∠OMN+∠BAN,原因如下:
如图2中,过N点作NH∥AB,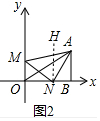
∵AB⊥X轴
∴AB∥OM
∴AB∥NH∥OM
∴∠OMN=∠MNH
∠BAN=∠ANH
∴∠ANM=∠MNH+∠ANH
=∠OMN+∠BAN.
②S四边形AMON=12,理由如下:
∵a=2
∴A(6,4)
∴OB=6,AB=4,OM=2t BN=3t
ON=6-3t
∴S四边形AMON=S四绞刑ABOM-S△ABN,
=$\frac{1}{2}$(AB+OM)×OB-$\frac{1}{2}$×BN×AB
=$\frac{1}{2}$(4+2t)×6-$\frac{1}{2}$×3t×4
=12+6t-6t
=12
∴四边形AMON的面积不变
(3)∵OM=ON
∴2t=6-3t或2t=3t-6
∴t=$\frac{6}{5}$或6.
点评 本题考查三角形综合题、平行线的性质、四边形的面积、一元一次方程等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考压轴题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
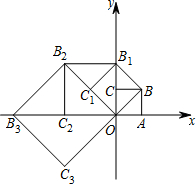 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).
如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则点B6的坐标为(8,-8).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | 3.14 | C. | 6.$\stackrel{••}{66}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
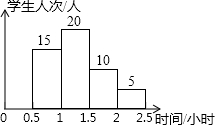 某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )| A. | 15 | B. | 20 | C. | 10 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{m}$ | B. | -m | C. | -$\sqrt{m}$ | D. | -$\sqrt{-m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6$\sqrt{\frac{a}{2}}$=$\sqrt{3a}$ | B. | -2$\sqrt{3}$=$\sqrt{(-2)^{2}×3}$ | C. | a2$\sqrt{\frac{1}{a}}$=$\sqrt{a}$ | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com