Question

10．如图，在等边△ABC中，边长为30，点M为线段AB上一动点，将等边△ABC沿过M的直线折叠，折痕与直线AC交于点N，使点A落在直线BC上的点D处，且BD：DC=1：4，设折痕为MN，则AN的值为21或65．

Answer 1

分析 此题要分两种情况进行讨论：：①当点A落在线段BC上时；②当A在CB的延长线上时，首先证明△BMD∽△CDN．根据相似三角形的性质可得$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$，再设AN=x，则CN=30-x，然后利用含x的式子表示DM、BM，根据BM+DM=30列出方程，解出x的值可得答案．

解答 解：①当点A落在如图1所示的位置时，
∵△ACB是等边三角形，
∴∠A=∠B=∠C=∠MDN=60°，
∵∠MDC=∠B+∠BMD，∠B=∠MDN，
∴∠BMD=∠NDC，
∴△BMD∽△CDN．
∴$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$，
∵DN=AN，
∴$\frac{BD}{CN}$=$\frac{DN}{AN}$=$\frac{BM}{CD}$，
∵BD：DC=1：4，BC=30，
∴DB=6，CD=24，
设AN=x，则CN=30-x，
∴$\frac{6}{30-x}$=$\frac{DM}{x}$=$\frac{BM}{24}$，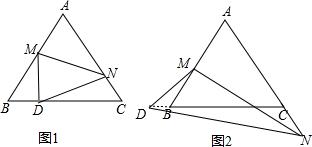
∴DM=$\frac{6x}{30-x}$，BM=$\frac{72}{30-x}$，
∵BM+DM=30，
∴$\frac{6x}{30-x}$+$\frac{72}{30-x}$=30，
解得x=21，
∴AN=21；

②当A在CB的延长线上时，如图2，
与①同理可得△BMD∽△CDN．
∴$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$，
∵BD：DC=1：4，BC=30，
∴DB=10，CD=40，
设AN=x，则CN=x-30，
∴$\frac{10}{x-30}$=$\frac{DM}{x}$=$\frac{BM}{40}$，
∴DM=$\frac{10x}{x-30}$，BM=$\frac{200}{x-30}$，
∵BM+DM=30，
∴$\frac{10}{x-30}$+$\frac{200}{x-30}$=15，
解得：x=65，
∴AN=65．
故答案为：21或65．

点评 此题主要考查了翻折变换，关键是证明△BMD∽△CDN得到$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$，再利用含AN的式子表示DM、BM．