
 ��֪����x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0����������ȵ�ʵ������kΪ��������
��֪����x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0����������ȵ�ʵ������kΪ������������ ��1�����ݡ���0���г�����ʽ���ɽ�����⣮
��2�����÷��������A��B�������꣬ȷ���Ա���x��ȡֵ��Χ���������κ��������ö��κ��������ʼ��ɽ�����⣮
��� �⣺��1���߹���x��һԪ���η���x2+2x+$\frac{k-1}{2}$=0����������ȵ�ʵ������
���=b2-4ac=4-4��$\frac{k-1}{2}$��0��
��k-1��2��
��k��3��
��k��������
��kΪ1��2��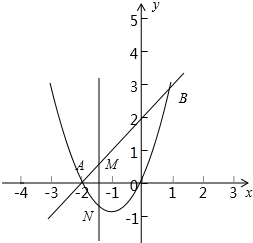
��2����x=0���뷽��x2+2x+$\frac{k-1}{2}$=0��k=1��
����κ���Ϊy=x2+2x��
��$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$ ��$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$��
��ֱ��y=x+2����κ���y=x2+2x�Ľ���ΪA��-2��0����B��1��3��
���������M��m��m+2��������-2��m��1����N��m��m2+2m����
MN=m+2-��m2+2m��=-m2-m+2=-��m+$\frac{1}{2}$��2+$\frac{9}{4}$��
�൱m=-$\frac{1}{2}$ʱ��MN�ij������ֵΪ$\frac{9}{4}$��
��ʱ��M������Ϊ��-$\frac{1}{2}$��$\frac{3}{2}$����
���� ���⿼����κ����ۺ��⡢һ�κ�����һԪ���η��̵��б�ʽ��֪ʶ������Ĺؼ���ѧ��ת����˼��˼�����⣬������ת��Ϊ����ʽ�����κ�������������п��������ͣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
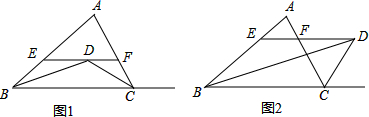
 ��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DF��AB������ΪF��DE=DG����ADG�͡�AED������ֱ�Ϊ49��40�����EDF�����Ϊ���٣�
��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DF��AB������ΪF��DE=DG����ADG�͡�AED������ֱ�Ϊ49��40�����EDF�����Ϊ���٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com