
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
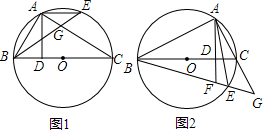
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
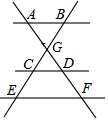 如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )
如图.AB∥CD∥EF,AF、BE交于点G,下列比例式错误的是( )| A. | $\frac{AD}{DF}=\frac{BC}{CE}$ | B. | $\frac{AG}{GD}=\frac{BG}{CG}$ | C. | $\frac{GC}{GE}=\frac{CD}{EF}$ | D. | $\frac{AB}{EF}=\frac{AG}{GE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 任意打开九年级上册数学教科书,正好是56页是确定事件 | |
| D. | 一只盒子中有白球m个,红球5个,黑球n个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
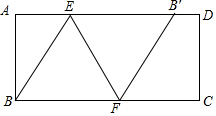 在矩形ABCD中(四个角都是直角,AD=BC,AB=CD),将矩形折叠,使点B落在边AD上B’处,这时折痕与边AD和BC分别交于点E、点F.然后再展开铺平,以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.
在矩形ABCD中(四个角都是直角,AD=BC,AB=CD),将矩形折叠,使点B落在边AD上B’处,这时折痕与边AD和BC分别交于点E、点F.然后再展开铺平,以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
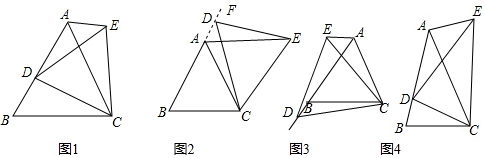
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com