
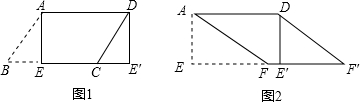
���� ��1�����ݾ��ε��ж����ɵô𰸣�
��2���ٸ������ε��ж����ɵô𰸣�
�ڸ��ݹ��ɶ������ɵô𰸣�
��� �⣺��1����ͼ1��ֽƬ?ABCD�У�AD=5��S?ABCD=15������A��AE��BC������ΪE����AE���¡�ABE������ƽ������DCE���λ�ã�ƴ���ı���AEE��D�����ı���AEE��D����״Ϊ���Σ�
��ѡ��C��
��2����֤������ֽƬ?ABCD�У�AD=5��S?ABCD=15������A��AE��BC������ΪE��
��AE=3��
��ͼ2�� ��
��
�ߡ�AEF������ƽ������DE��F�䣬
��AF��DF�䣬AF=DF�䣬
���ı���AFF��D��ƽ���ı��Σ�
��Rt��AEF�У��ɹ��ɶ�������
AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��AF=AD=5��
���ı���AFF��D�����Σ�
������AF�䣬DF����ͼ3��
��Rt��DE��F��E��F=FF��-E��F��=5-4=1��DE��=3��
��DF=$\sqrt{E{��D}^{2}+E��{F}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$��
��Rt��AEF����EF��=EF+FF��=4+5=9��AE=3��
��AF��=$\sqrt{A{E}^{2}+F��{E}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$��
���� ���⿼����ͼ�εļ�ƴ�������˾��ε��ж������ε��ж������ɶ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
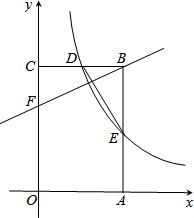 ��ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y=$\frac{k}{x}$��x��0������ͼ��BC�ϵĵ�D��AB���ڵ�E������DE������E��AB���е�q
��ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y=$\frac{k}{x}$��x��0������ͼ��BC�ϵĵ�D��AB���ڵ�E������DE������E��AB���е�q�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������ABCD�У�AB��CD����E��F��G�ֱ���BD��AC��DC���е㣬��֪���ײ���8����������16�����EFG���ܳ���12��
��֪������ABCD�У�AB��CD����E��F��G�ֱ���BD��AC��DC���е㣬��֪���ײ���8����������16�����EFG���ܳ���12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
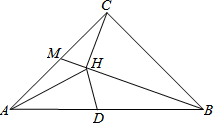 �ڡ�ABC�У���ACB=90�㣬AC=BC=2��M�DZ�AC���е㣬CH��BM��H��
�ڡ�ABC�У���ACB=90�㣬AC=BC=2��M�DZ�AC���е㣬CH��BM��H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
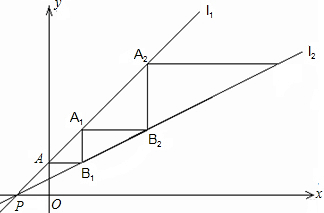 ��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=$\frac{1}{2}$x+$\frac{1}{2}$�ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶����ﵽֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������B2015��A2015��������C����A2015��ʱ���˶�����·���ij�Ϊ��������
��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=$\frac{1}{2}$x+$\frac{1}{2}$�ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶����ﵽֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������B2015��A2015��������C����A2015��ʱ���˶�����·���ij�Ϊ��������| A�� | 22015-2 | B�� | 22014-1 | C�� | 22016-2 | D�� | 22017-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
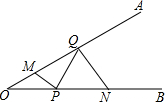 ��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ���OM=1��ON=3����P��Q�ֱ��ڱ�OB��OA�ϣ���MP+PQ+QN����Сֵ��$\sqrt{10}$��
��ͼ����AOB=30�㣬��M��N�ֱ��ڱ�OA��OB�ϣ���OM=1��ON=3����P��Q�ֱ��ڱ�OB��OA�ϣ���MP+PQ+QN����Сֵ��$\sqrt{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
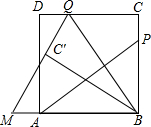 ��ͼ��PΪ������ABCD�ı�BC��һ���㣨P��B��C���غϣ�������AP������B��BQ��AP��CD�ڵ�Q������BQC��BQ���ڵ�ֱ�߶��۵õ���BQC�䣬�ӳ�QC�佻BA���ӳ����ڵ�M��
��ͼ��PΪ������ABCD�ı�BC��һ���㣨P��B��C���غϣ�������AP������B��BQ��AP��CD�ڵ�Q������BQC��BQ���ڵ�ֱ�߶��۵õ���BQC�䣬�ӳ�QC�佻BA���ӳ����ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
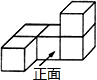 ��ͼ��ʾ�ļ������������С��������϶��ɵģ���������ͼ�ǣ�������
��ͼ��ʾ�ļ������������С��������϶��ɵģ���������ͼ�ǣ�������| A�� | 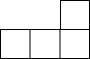 | B�� | 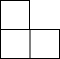 | C�� | 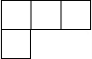 | D�� | 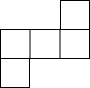 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com