
分析 首先将括号里面进行通分,进而将能分解因式的分解因式,再化简求出答案.
解答 解:($\frac{{x}^{2}-y}{x}$-x-1)÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-2xy+{y}^{2}}$,
=($\frac{{x}^{2}-y}{x}$-$\frac{{x}^{2}}{x}$-$\frac{x}{x}$)×$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=$\frac{-y-x}{x}$×$\frac{x-y}{x+y}$
=-$\frac{x-y}{x}$,
把x=$\sqrt{2}$,y=$\sqrt{6}$代入得:
原式=-$\frac{\sqrt{2}-\sqrt{6}}{\sqrt{2}}$=-1+$\sqrt{3}$.
点评 此题主要考查了分式的化简求值,正确因式分解是解题关键.


科目:初中数学 来源: 题型:选择题
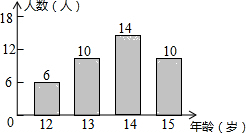 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )| A. | 12岁 | B. | 13岁 | C. | 14岁 | D. | 15岁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com