
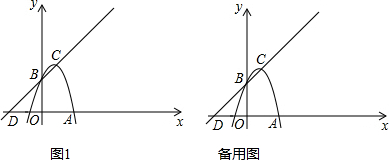
���� ��1����y=0����õ�A�����꣬Ȼ�������䷽���Ͷ������깫ʽ����������ߵĶ���C�����ꣻ
��2������õ�B�����꣬Ȼ�������ô���ϵ�������BC�Ľ���ʽ��ֱ��BC�Ľ���ʽ����E��a��a+3������l2�Ľ���ʽΪy=-��x-a��2+a+3��������������A��������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ�������l2�Ľ���ʽ������P1CE=90��ʱ�������CP1�Ľ���ʽ���Ӷ�����õ�P1�����꣬ͬ�������P2�����ꣻ��ͼ3��ʾ����CEΪֱ����ԲG������G��GF��x�ᣬ����ΪF�������FG��CE�ij���Ȼ�����d��r�Ĺ�ϵ�����ԲG��x���λ�ù�ϵ�����жϡ�CP3E��Ϊֱ�������Σ�
��� �⣺��1������y=0�ã�x2-2x-3=0������x-3����x+1��=0����ã�x1=-1��x2=3��
���A��������3��0����
��y=-x2+2x+3=-��x2-2x��+3=-��x2-2x+1-1��+3=-��x-1��2+4��
���C��1��4����
��2����ֱ��CD�Ľ���ʽΪy=kx+b��
��CD������C��1��4����B��0��3����
��$\left\{\begin{array}{l}{k+b=4}\\{b=3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$��
��ֱ��CD����ʽΪy=x+3��
��������l2��������l1��ֱ��BC����ƽ�Ƶõ���
�ඥ��E��ֱ��BC�ϣ�
��E��a��a+3������������l2�Ľ���ʽΪy=-��x-a��2+a+3��
��������l2����A��3��0����
��-��3-a��2+a+3=0����ã�a1=6��a2=1����ȥ����
��������l2�Ľ���ʽΪy=-��x-6��2+9=-x2+12x-27��
������l2�Ĵ���ͼ����ͼ1��ʾ��
��ͼ2��ʾ������P1CE=90��ʱ��
��ֱ��CP1�Ľ���ʽΪy=kx+b��
��CP1��BC��
��k=-1��
��y=-x+b��
�߽���C��1��4������ã�-1+b=4�����b=5��
��ֱ��CP1�Ľ���ʽΪy=-x+5��
��y=0�ã�-x+5=0�����x=5��
���P1��������5��0����
��ֱ��EP2�Ľ���ʽΪy=-x+b��
�߽���E��6��9������ã�-6+b=9����ã�b=15��
��ֱ��EP2�Ľ���ʽΪy=-x+15��
����y=0�ã�-x+15=0����ã�x=15��
���P2��������15��0����
��ͼ3��ʾ����CEΪֱ����ԲG������G��GF��x�ᣬ����ΪF��
��C��1��4����E��6��9����
��G��3.5��6.5����
��GF=6.5��
���������ľ��빫ʽ��֪CE=$\sqrt{��6-1��^{2}+��9-4��^{2}}$=5$\sqrt{2}$��
��r=$\frac{5\sqrt{2}}{2}$��
��d��r��
��ԲG��x�����룮
���CP3E��90�㣬��ʱ���ܹ���ֱ�������Σ�
������������P��������5��0����15��0����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ�����һ�κ����Ľ���ʽ��ֱ�ߺ�Բ��λ�ù�ϵ�������ľ��빫ʽ�����������ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
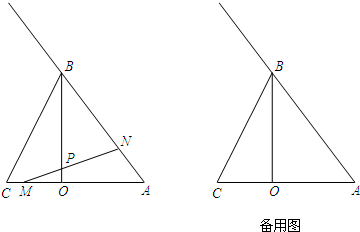
 ��ͼ����֪A��2$\sqrt{3}$��2����B��2$\sqrt{3}$��1��������AOB���ŵ�O��ʱ����ת90�㣬�����A��B��O��λ�ã���ͼ��ͼ��ABB��A����ܳ�Ϊ$\frac{\sqrt{13}}{2}$��+2��+2��
��ͼ����֪A��2$\sqrt{3}$��2����B��2$\sqrt{3}$��1��������AOB���ŵ�O��ʱ����ת90�㣬�����A��B��O��λ�ã���ͼ��ͼ��ABB��A����ܳ�Ϊ$\frac{\sqrt{13}}{2}$��+2��+2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
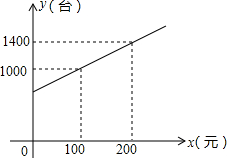 Ϊ���������裬�û���ũ�ḻũ���ҵ����������Ͳʵ����磬���Ҿ���ʵ�������������涨ÿ����һ̨�ʵ磬������������Ԫ��������ij�̳����۲ʵ�̨��y��̨���벹�����x��Ԫ��֮�����������ͼ��ʾ��һ�κ�����ϵ�����Ų������x�IJ�������������Ҳ�������ӣ���ÿ̨�ʵ������p��Ԫ������Ӧ���������㣺p=-$\frac{1}{5}$x+110��x��0����
Ϊ���������裬�û���ũ�ḻũ���ҵ����������Ͳʵ����磬���Ҿ���ʵ�������������涨ÿ����һ̨�ʵ磬������������Ԫ��������ij�̳����۲ʵ�̨��y��̨���벹�����x��Ԫ��֮�����������ͼ��ʾ��һ�κ�����ϵ�����Ų������x�IJ�������������Ҳ�������ӣ���ÿ̨�ʵ������p��Ԫ������Ӧ���������㣺p=-$\frac{1}{5}$x+110��x��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com