
分析 先令y=0,则-2x2-mx+6=0,设一元二次方程2x2+mx-6=0的两根分别为x1,x2,再根据根与系数的关系得出x1+x2与x1•x2的值,根据两交点间的线段长为4即可得出m的值.
解答 解:令y=0,则-2x2-mx+6=0,设一元二次方程2x2+mx-6=0的两根分别为x1,x2,则x1+x2=-$\frac{m}{2}$①,x1•x2=-$\frac{6}{2}$=-3②,
∵抛物线与x轴相交时两交点间的线段长为4,
∴|x1-x2|=4,
∴(x1-x2)2=16,即(x1+x2)2-4x1x2=16,
把①②代入得,(-$\frac{m}{2}$)2-4×(-3)=16,
解得m=±4.
故答案为:±4.
点评 本题考查的是抛物线与x轴的交点问题,熟知一元二次方程根与系数的关系是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
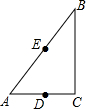 如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )
如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )| A. | 点A | B. | 点D | C. | 点C | D. | 点E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,
已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.
如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com